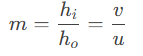A concave lens (or diverging lens) is a transparent optical device that is thinner at the center and thicker at the edges. It causes parallel light rays to diverge (spread out), making it useful in correcting vision problems and optical instruments.
Key Characteristics of a Concave Lens
✔ Diverges light rays (spreads them apart)
✔ Forms virtual, diminished, and erect images
✔ Used in correcting myopia (nearsightedness)
✔ Has a negative focal length
Section 1: Concave Lens Formula & Sign Convention
1.1 Lens Formula
The lens formula relates the object distance (u), image distance (v), and focal length (f):
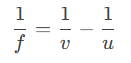
Where:
-
f= Focal length (always negative for concave lenses)
-
u = Object distance (negative if on the left side of the lens)
-
= Image distance (negative for virtual images)
1.2 Magnification Formula
-
If ∣m∣<1 → Image is diminished
-
If m is positive → Image is erect
Section 2: Image Formation by Concave Lens (Ray Diagrams)
Case 1: Object at Infinity
-
Rays: Parallel rays diverge after refraction.
-
Image: Virtual, highly diminished, at the focal point.
Case 2: Object Between Infinity and Optical Center
-
Rays: Diverging rays appear to come from a point between F and the lens.
-
Image: Virtual, diminished, erect.
Section 3: Uses of Concave Lenses
| Application | Explanation |
|---|---|
| Correcting Myopia | Diverges light before it enters the eye, helping focus images on the retina. |
| Peepholes in Doors | Provides a wide-angle view of outside visitors. |
| Laser Beam Expanders | Used with convex lenses to control beam spread. |
| Camera Lenses | Helps reduce aberrations in combination with convex lenses. |
Section 4: Concave Lens vs. Convex Lens
| Feature | Concave Lens | Convex Lens |
|---|---|---|
| Shape | Thinner at center, thicker at edges | Thicker at center, thinner at edges |
| Light Behavior | Diverges light rays | Converges light rays |
| Focal Length | Negative | Positive |
| Image Formed | Virtual, diminished, erect | Real or virtual, magnified or diminished |
Section 5: Numerical Problems (Solved Examples)
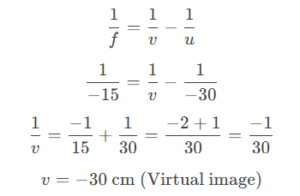
Example 1: Finding Image Position
Problem: A concave lens has a focal length of -15 cm. An object is placed 30 cm from the lens. Find the image position.
Solution:
Using lens formula:
Example 2: Magnification Calculation
Problem: An object 4 cm tall is placed 20 cm from a concave lens of focal length -10 cm. Find the image height.
Solution:
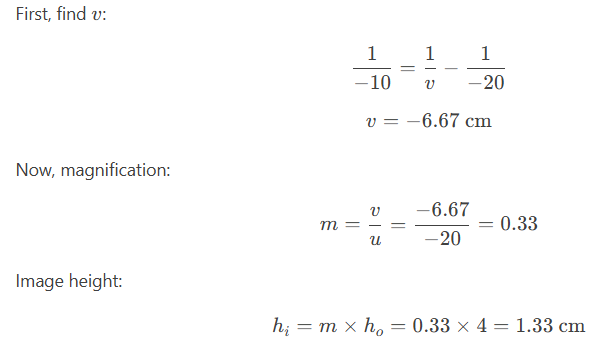
Section 6: FAQs on Concave Lenses
❓ Can a concave lens form a real image?
No, it always forms a virtual, erect, and diminished image.
❓ Why is the focal length negative?
Because the lens diverges light, and the focus is on the same side as the object.
❓ Where are concave lenses used in daily life?
In spectacles for myopia, cameras, telescopes, and door peepholes.
❓ How does a concave lens correct myopia?
It diverges light before it enters the eye, helping focus the image correctly on the retina.
Conclusion & Summary
Key Takeaways

Need Practice? Try these:
-
A concave lens (f=−12 cm) has an object placed 24 cm away. Find v.
-
Calculate the magnification if the image distance is −8 cm and object distance is −16 cm.