Class 8 Maths NCERT Solutions Chapter 9: Algebraic Expressions and Identities
Ex – 9.1
Question 1.
Identify the terms, their coefficients for each of the following expressions:
(i) 5xyz2−3zy
(ii) 1+x+x2
(iii) 4x2y2−4x2y2z2+z2
(iv) 3 – pq + qr – rp
(v) x2+y2−xy
(vi) 0.3a – 0.6ab + 0.5b.
Solution.
(i) 5xyz2−3zy

(ii) 1+x+x2
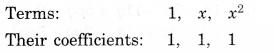
(iii) 4x2y2−4x2y2z2+z2
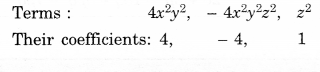
(iv) 3 – pq + qr – rp
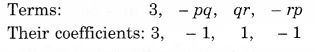
(v) x2+y2−xy

(vi)0.3a – 0.6ab + 0.5b.

Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?
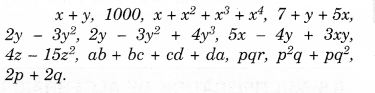
Solution.
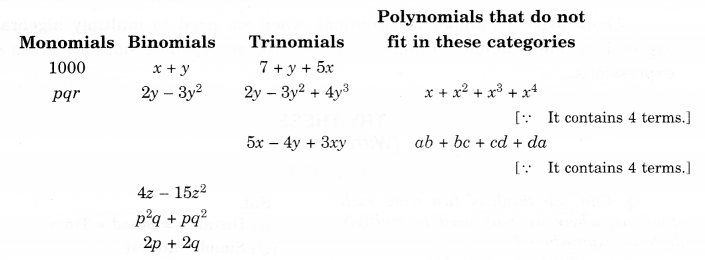
Question 3.
Add the following.
(i) ab – be, be – ca, ca – ab
(ii) a -b + ab, b – c + be, c – a + ac
(iii) 2p2q2−3pq+4,5+7pq−3p2q2
(iv) l2+m2,m2+n2,n2+l2, 2lm + 2mn + 2nl.
Solution.
(i) ab – be, be – ca, ca – ab
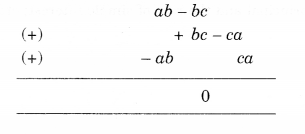
(ii) a -b + ab, b – c + be, c – a + ac
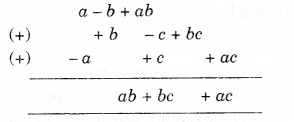
(iii) 2p2q2−3pq+4,5+7pq−3p2q2
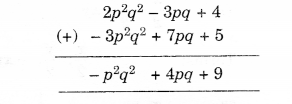
(iv) l2+m2,m2+n2,n2+l2, 2lm + 2mn + 2nl.
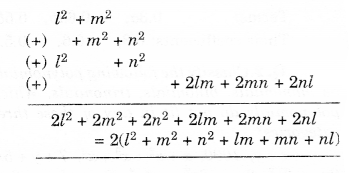
Question 4.
(a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 56 – 3
(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract 4p2q−3pq+5pq2−8p+7q−10 from 18−3p−11q+5pq−2pq2+5p2q
Solution.
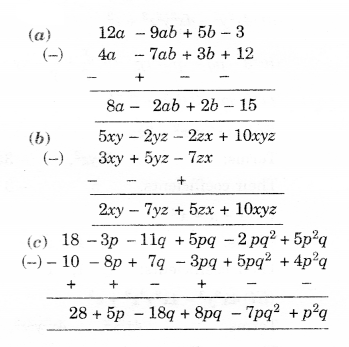
Ex – 9.2
Question 1.
Find the product of the following pairs of monomials:
(i) 4, 7p
(ii) – 4p, 7p
(iii) – 4p, 7pq
(iv) 4p3,,−3p
(v) 4p, 0.
Solution.
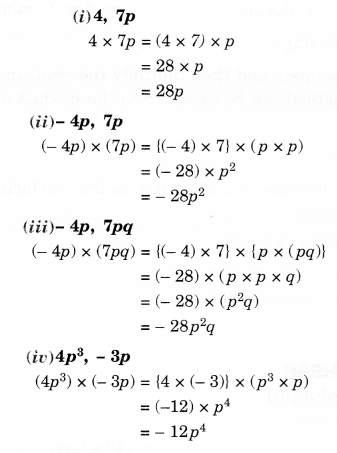
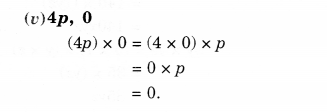
Question 2.
Find the areas of rectangles with the following pairs of mononials as their lengths and breadths respectively:
(i) (p, q);
(ii) (10m, 5n);
(iii) (20x2,5y2);
(iv) (4x,3x2);
(v) (3mn, 4np).
Solution.
(i) (p, q)
Length = p
Breadth = q
∴ Area of the rectangle
= Length x Breadth
= pxq
= pq
(ii) (10m, 5n)
Length = 10 m
Breadth = 5 n
∴ Area of the rectangle
= Length x Breadth
= (10m) x (5n)
= (10 x 5) x (m x n)
= 50 x (mn)
= 50 mn
(iii) (20x2,5y2)
Length = 20x2
Breadth = 5y2
∴ Area of the rectangle
= Length x Breadth
= (20x2) x (5y2)
= (20 x 5) x (x2×y2)
= 100 x (x2y2)
= 100x2y2
(iv) (4x, 3xP)
Length = 4.x
Breadth = 3x2
∴ Area of the rectangle
= Length x Breadth =
(4x) x (3x2)
= (4 x 3) x (x×x2)
= 12 x x3
= 12×3
(v) (3mn, 4np)
Length = 3 mn
Breadth = 4np
∴ Area of the rectangle
= Length x Breadth
= (3mn) x (4np)
= (3 x 4) x (mn) x (np)
= 12 x m x (n x n) x p
= 12mn2p
Question 3.
Complete the table of products.
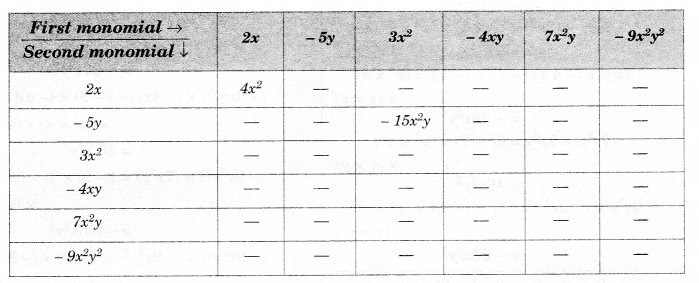
Solution.
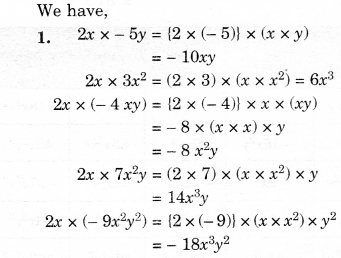
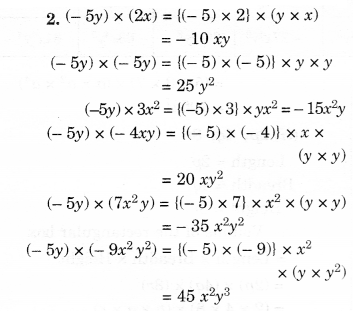
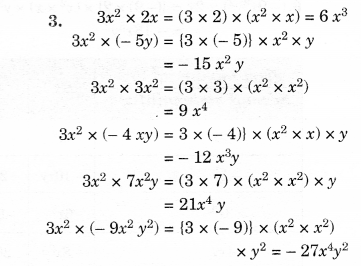
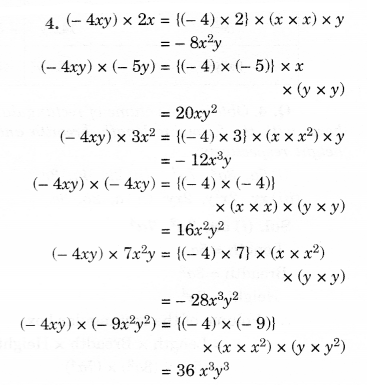
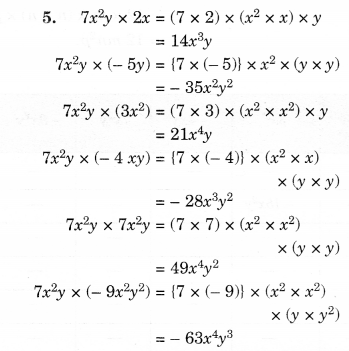
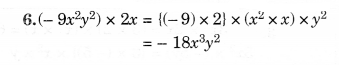
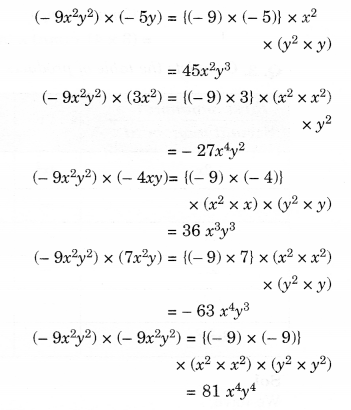
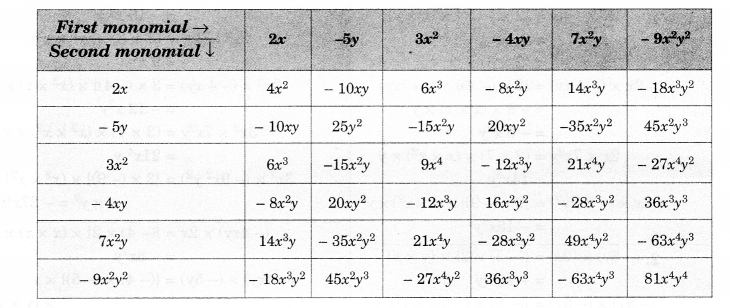
Question 4.
Obtain the volume of rectangular boxes with the following length, breadth and height respectively:
(i) 5a,3a2,7a4
(ii) 2p, 4q, 8r
(iii) xy,2x2y,2xy2
(iv) a, 2b, 3c
Solution.
(i) 5a,3a2,7a4
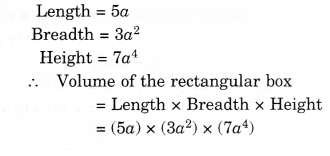
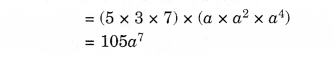
(ii) 2p, 4q, 8r
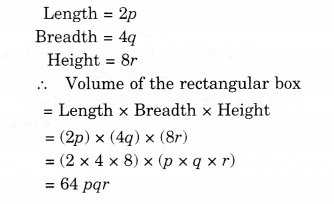
(iii) xy,2x2y,2xy2
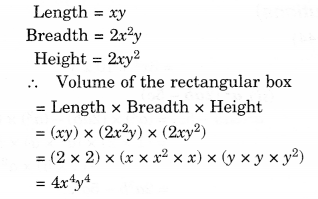
(iv) a, 2b, 3c
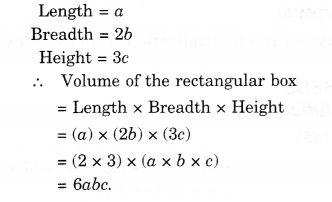
Question 5.
Obtain the product of
(i) xy, yz, zx
(ii) a,−a2,a3
(iii) 2,4y,8y2,16y3
(iv) a, 2b, 3c, 6abc
(v) m, – mn, mnp.
Solution.
(i) xy, yz, zx
Required product
= (xy) x (yz) x (zx)
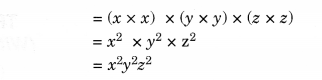
(ii) a,−a2,a3
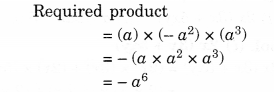
(iii) 2,4y,8y2,16y3
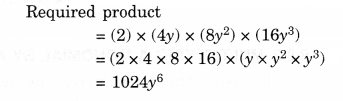
(iv) a, 2b, 3c, 6abc
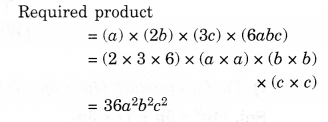
(v) m, – mn, mnp.
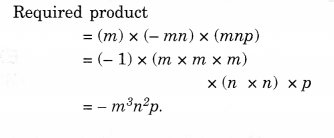
Ex – 9.3
Question 1.
Carry out the multiplication of the expressions in each of the following pairs:
(i) 4p, q + r
(ii) ab, a – b
(iii) a+b,7a2b2
(iv) a2−9,4a
(v) pq + qr + rp, 0
Solution.
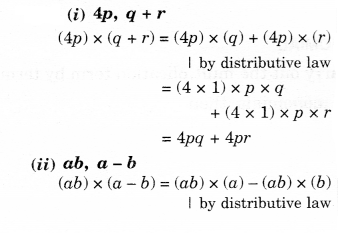
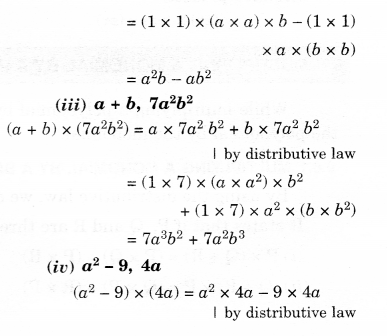
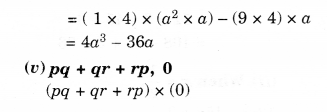
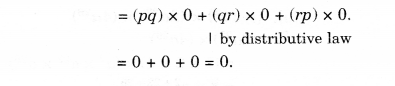
Question 2.
Complete the table

Solution.
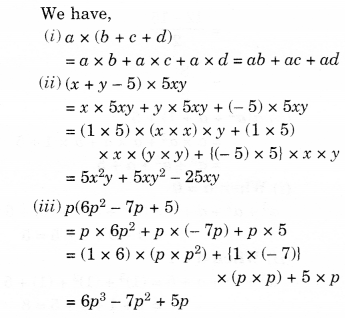
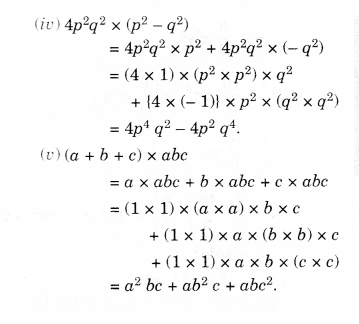

Question 3.
Find the product:
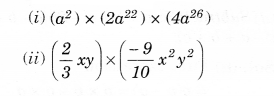
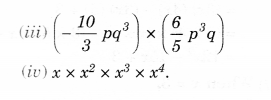
Solution.
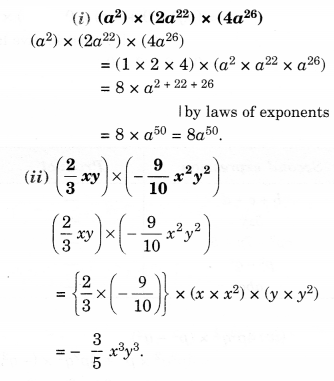
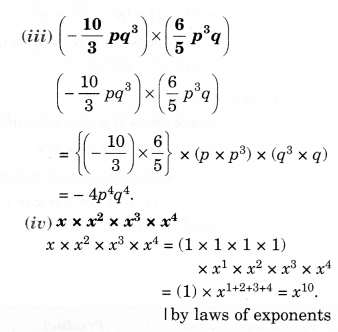
Question 4.
(a) Simplify: 3x (4x – 5) + 3 and find its values for (i) x = 3, (ii) x=12
(b) Simplify: a(a2+a+1)+5 and find its value for (i)a = 0, (ii)a = 1 and (iii) a = -1.
Solution.
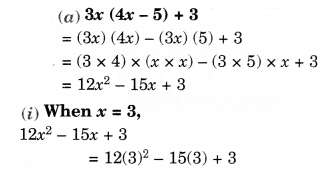
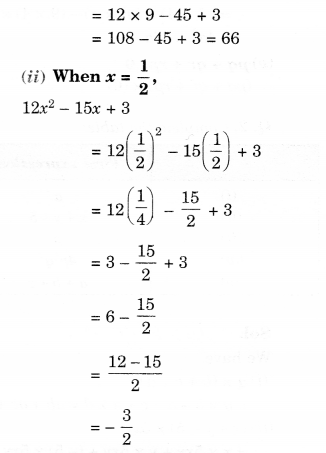
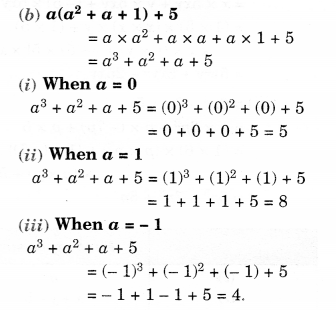
Question 5.
(a) Add: p(p – q), q(q – r) and r(r -p)
(b) Add: 2x(z – x – y) and 2y (z – y – x)
(c) Subtract: 3l (l – 4m + 5n) from 4l (10n – 3m + 2l)
(d) Subtract: 3a(a + b + c) – 2b(a – b + c) from 4c(- a + b + c).
Solution.
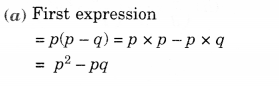
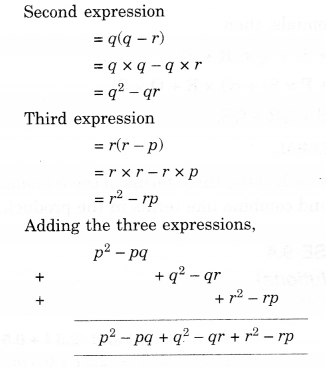
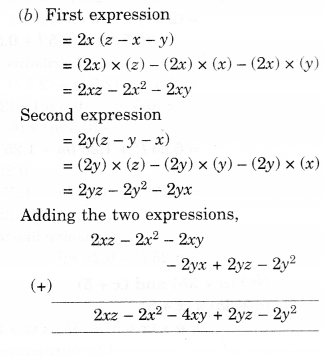


Ex – 9.4
Question 1.
Multiply the binomials:
(i) (2x + 5) and (4x – 3)
(ii) (y – 8) and (3y – 4)
(iii) (2.5l – 0.5 m) and (2.5l + 0.5m)
(iv) (a + 3b) and (x + 5)
(v) (2pq+3q2)and(3pq−2q2)
(vi) (34a2+3b2)and4(a2−23b2)
Solution.
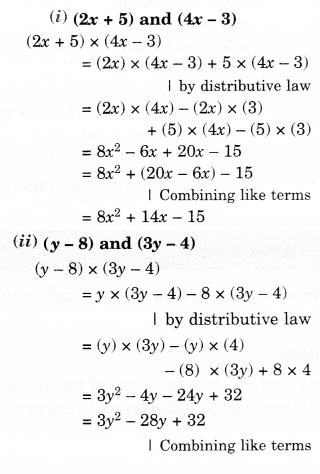

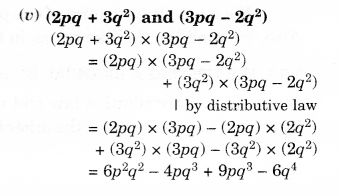
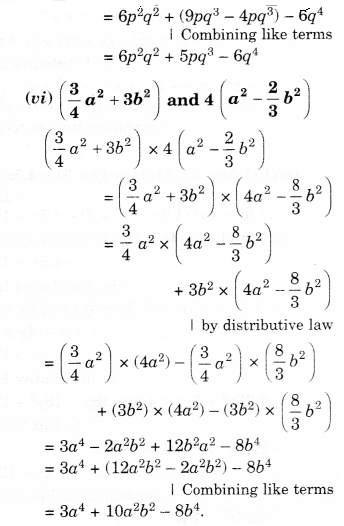
Question 2.
Find the product:
(i) (5 – 2x) (3 + x)
(ii) (x + 7y) (7x —y)
(iii) (a2+b)(a+b2)
(iv) (p2−q2)(2p+q)
Solution.
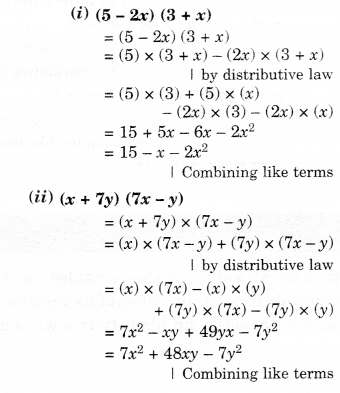
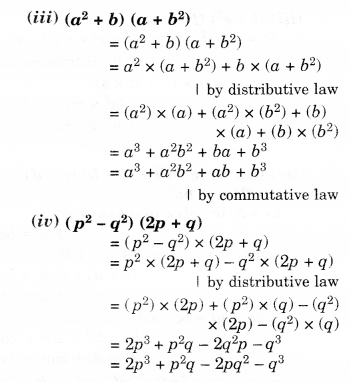
Question 3.
Simplify.
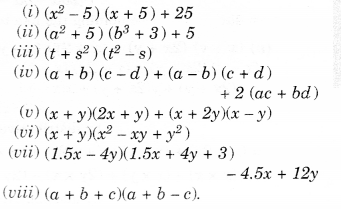
Solution.
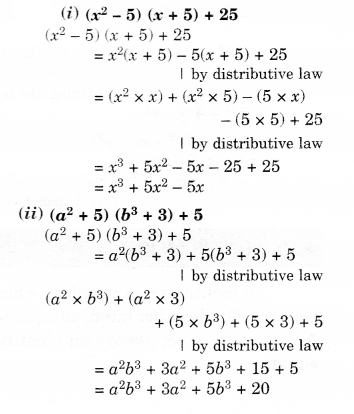
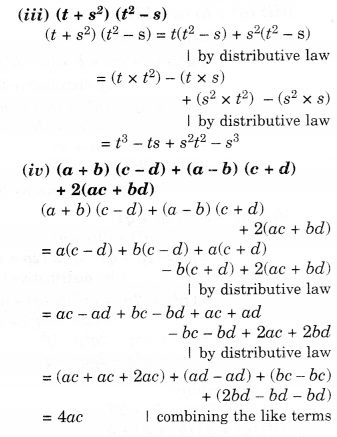
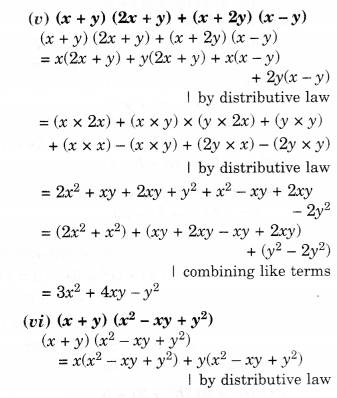
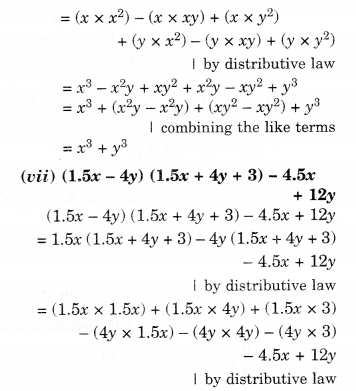

Ex – 9.5
Question 1.
Use a suitable identity to get each of the following products:
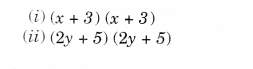
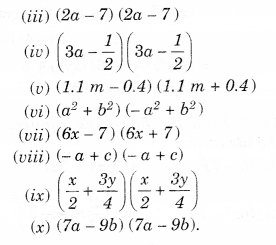
Solution.
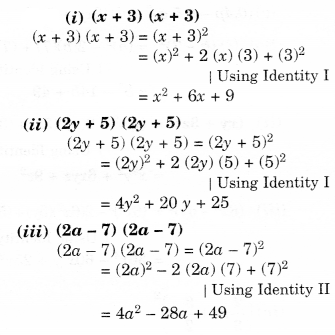



Question 2.
Use the identity (x+a)(x+b)=x2+(a+b)x+ab to find the following products:
(i) (x + 3) (x + 7)
(ii) (4x + 5) (4x + 1)
(iii) (4x – 5) (4x – 1)
(iv) (4x + 5) (4x – 1)
(v) (2x + 5y) (2x + 3y)
(vi) (2a2+9)(2a2+5)
(vii) (xyz – 4) (xyz – 2).
Solution.
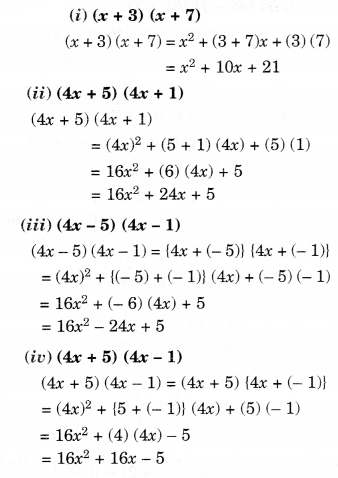
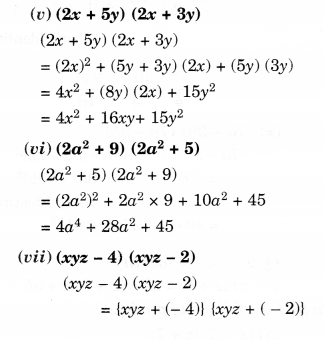
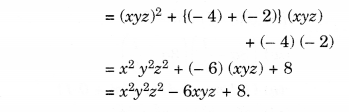
Question 3.
Find the following squares by using the identities.
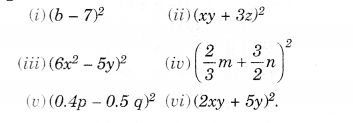
Solution.


Question 4.
Simplify:
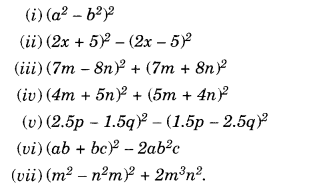
Solution.
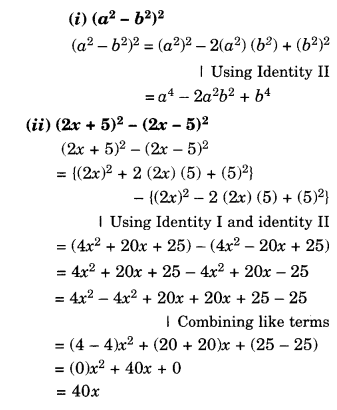
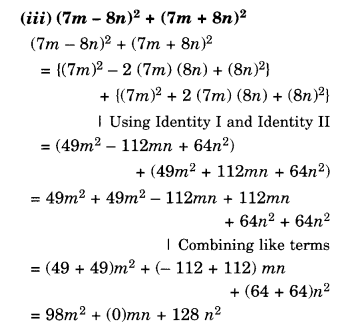
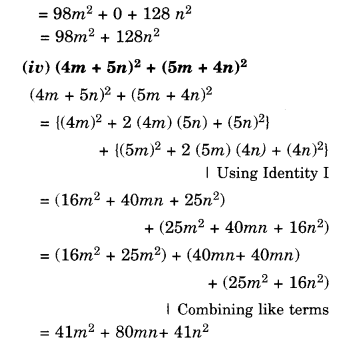
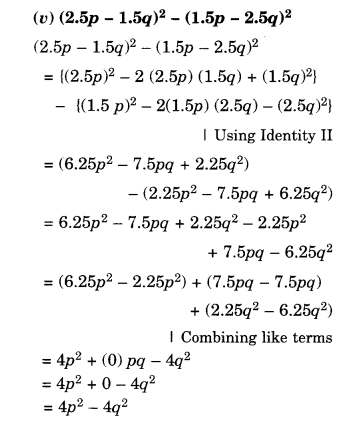
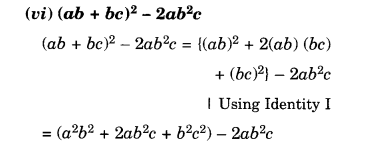
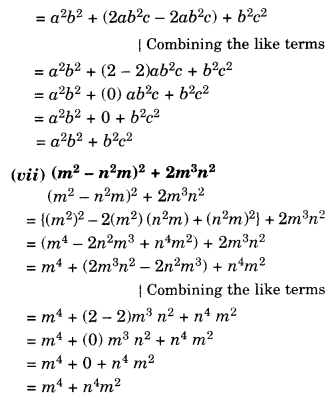
Question 5.
Show that:
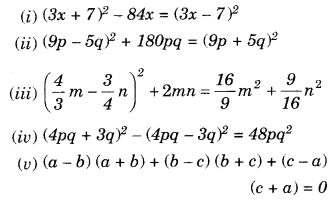
Solution.
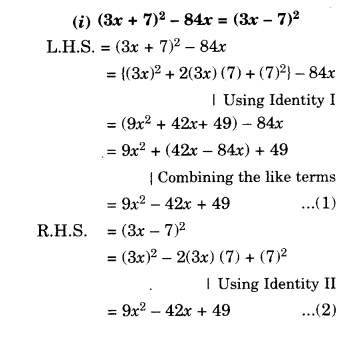


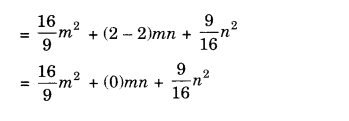
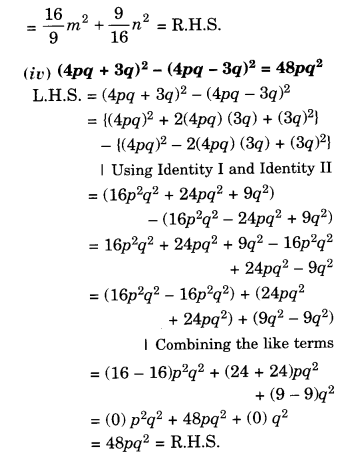
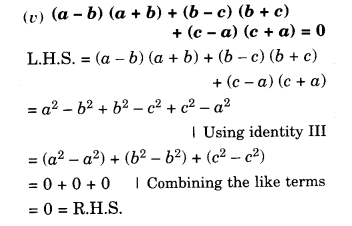
Question 6.
Using identities, evaluate:

Solution.
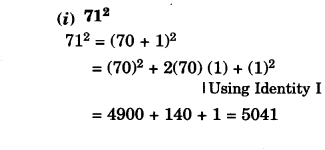



Question 7.
Using a2−b2=(a+b)(a−b), find
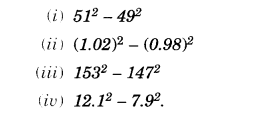
Solution.

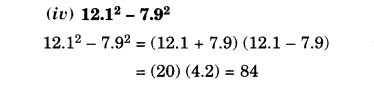
Question 8.
Using (x+a)(x+b)=x2+(a+b)x+ab, find
(i) 103 x 104
(ii) 5.1 x 5.2
(iii) 103 x 98
(iv) 9.7 x 9.8
Solution.

