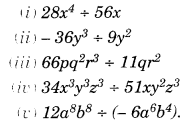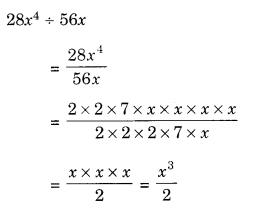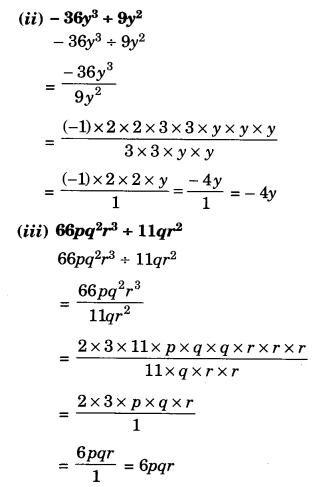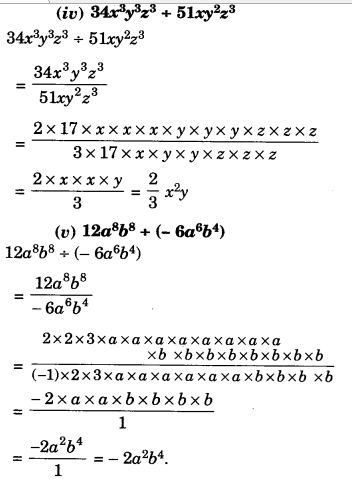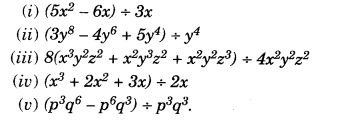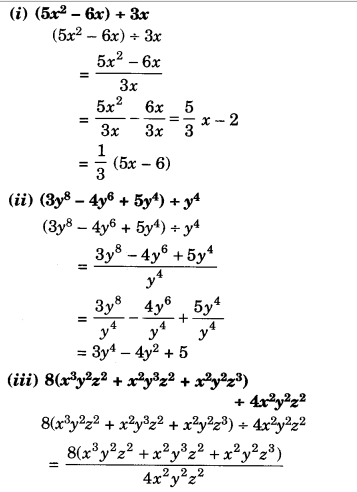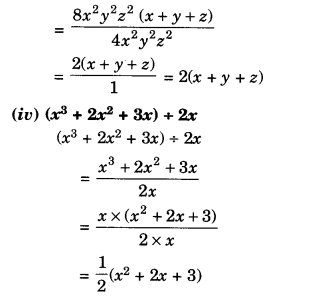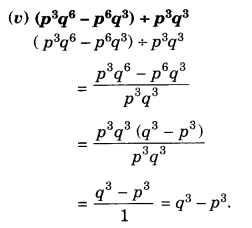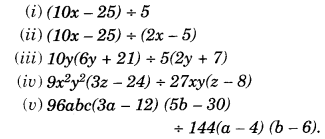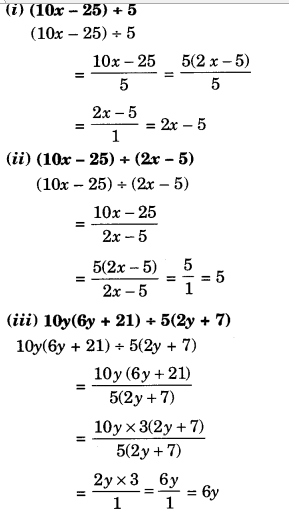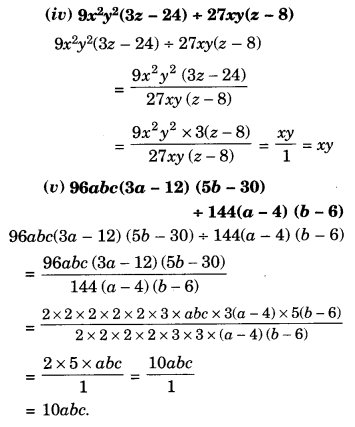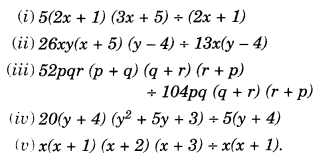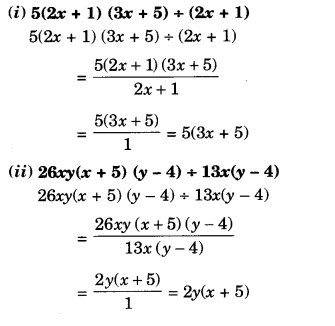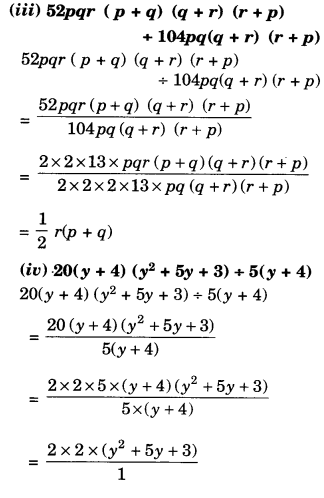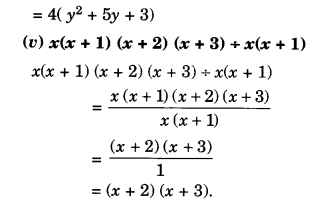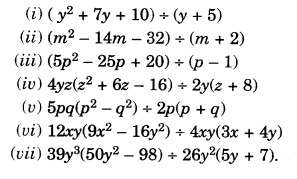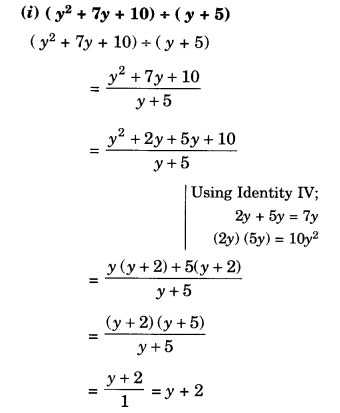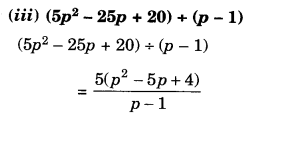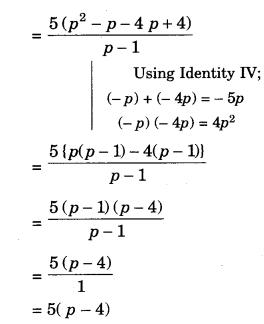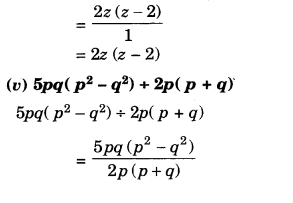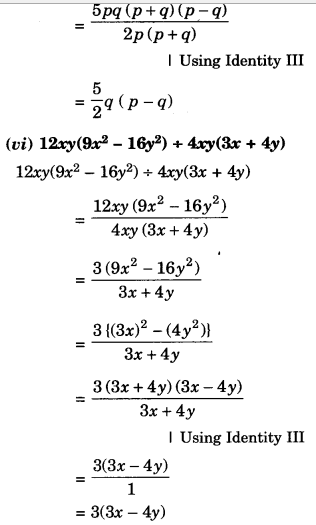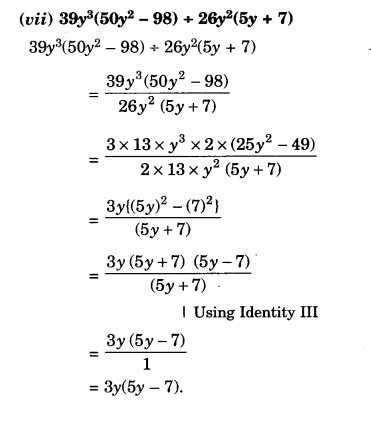Class 8 Maths NCERT Solutions Chapter 14: Factorisation
Ex – 14.1
Question 1.
Find the common factors of the given terms:
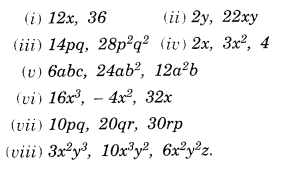
Solution.


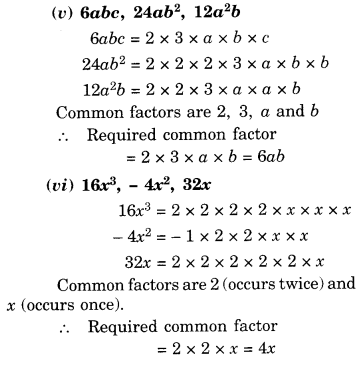

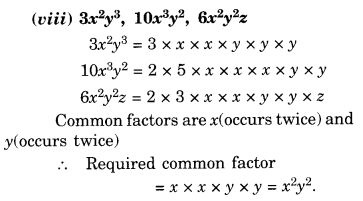
Question 2.
Factorise the following expressions:
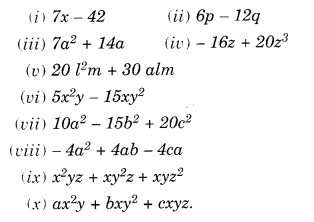
Solution.
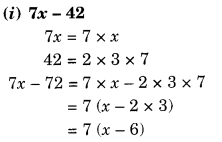
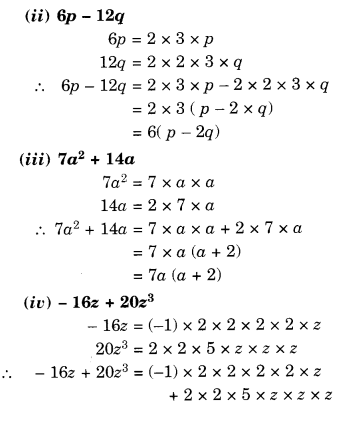
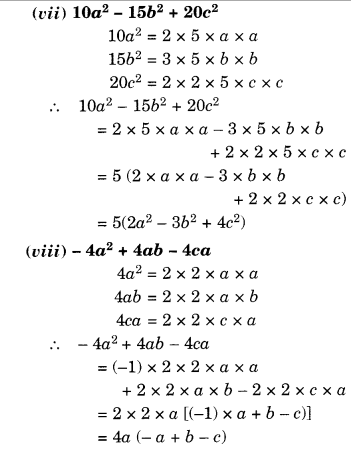
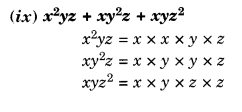
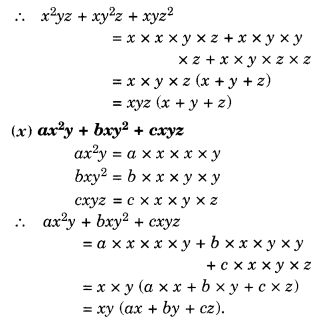
Question 3.
Factorise:
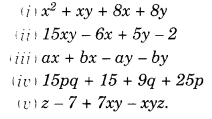
Solution.
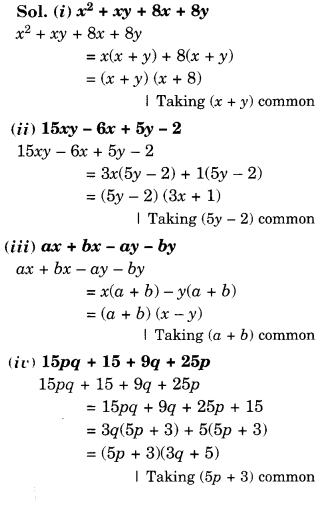
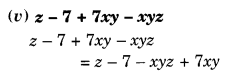
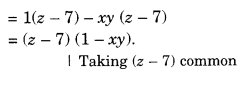
Ex – 14.2
Question 1.
Factorise the following expressions:
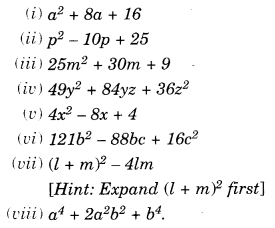
Solution.
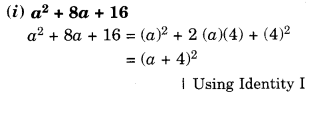

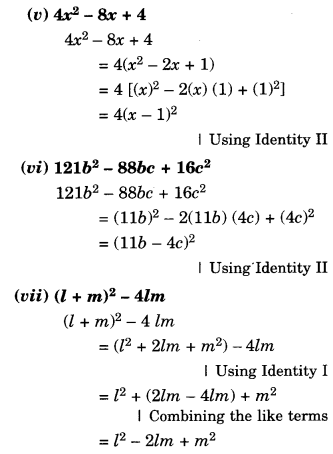
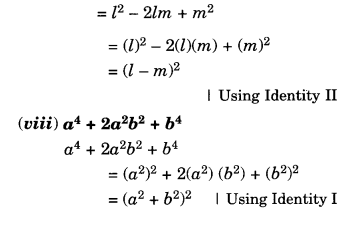
Question 2.
Factorise:
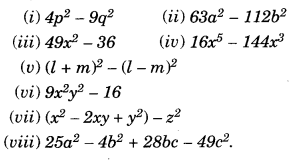
Solution.
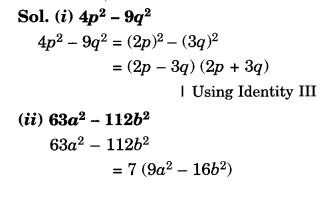
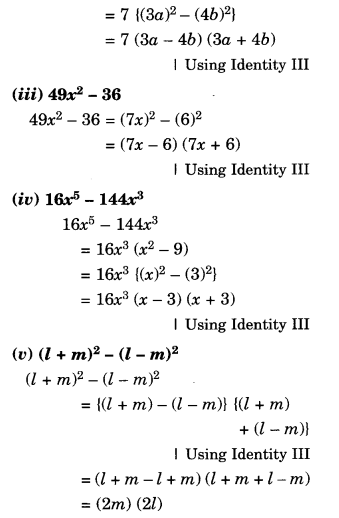

Question 3.
Factorise the expressions:
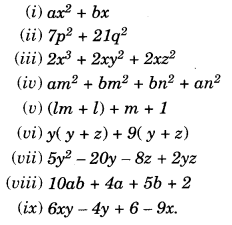
Solution.
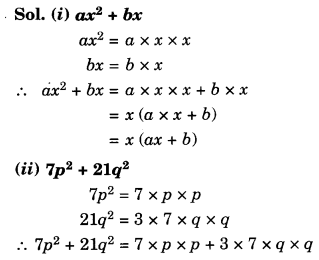
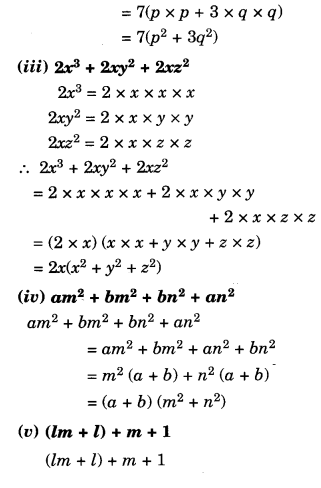
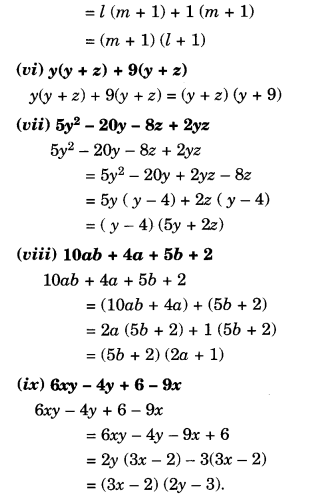
Question 4.
Factorise:
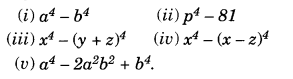
Solution.
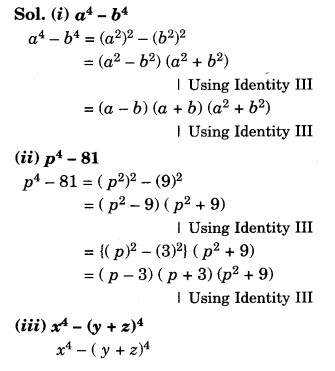
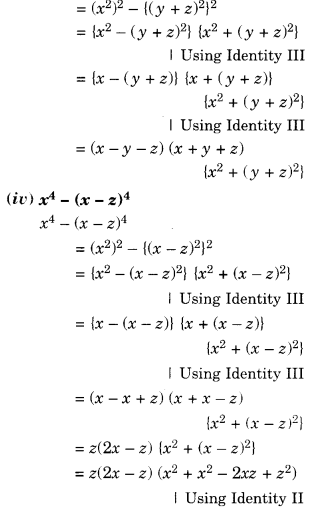

Question 5.
Factorise the following expressions:
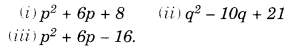
Solution.


Ex – 14.4
Find and correct the errors in the following mathematical statements.
Question 1.
4(x – 5) = 4x – 5
Solution.
4(x – 5) = 4x – 20
Question 2.
x(3x + 2) = { 3x }^{ 2 }+2
Solution.
x(3x + 2) = { 3x }^{ 2 }+2x
Question 3.
2x + 3y = 5xy
Solution.
2x + 3y = 2x + 3y
Question 4.
x + 2x + 3x = 5x
Solution.
x + 2x + 3x = 6x
Question 5.
5y + 2y + y – 7y = 0
Solution.
5y + 2y + y – 7y – y
Question 6.
3x + 2x = { 5x }^{ 2 }
Solution..
3x + 2x = 5x
Question 7.
{ \left( 2x \right) }^{ 2 } + 4(2x) + 7 = { 2x }^{ 2 } + 8x + 7
Solution.
{ \left( 2x \right) }^{ 2 } + 4(2x) + 7 = { 4x }^{ 2 } + 8x + 7
Question 8.
{ \left( 2x \right) }^{ 2 } + 5x = 4x + 5x = 9x
Solution.
{ \left( 2x \right) }^{ 2 } + 5x = { 4x }^{ 2 } + 5x
Question 9.
{ \left( 3x+2 \right) }^{ 2 } = { 3x }^{ 2 } + 6x + 4.
Solution.
{ \left( 3x+2 \right) }^{ 2 } = { 9x }^{ 2 }+ 12x + 4.
Question 10.
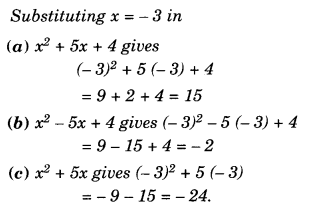
Solution.
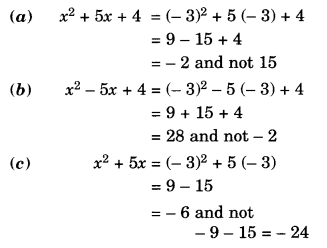
Question 11.
{ \left( y-3 \right) }^{ 2 } = { y }^{ 2 } – 9
Solution.
{ \left( y-3 \right) }^{ 2 } = { y }^{ 2 } – 2(y)(3) + { 3 }^{ 2 }
= { y }^{ 2 } – 6y + 9
and not equal to { y }^{ 2 } – 9
Question 12.
{ \left( z+5 \right) }^{ 2 } = { z }^{ 2 } + 25
Solution.
{ \left( z+5 \right) }^{ 2 } = { z }^{ 2 } + 2(z) (5) + { 5}^{ 2 }
= { z }^{ 2 } + 10z + 25
and not equal to { z }^{ 2 } + 25
Question 13.
\left( 2a+36 \right) \left( a-b \right) = { 2a }^{ 2 }-{ 3b }^{ 2 }
Solution.
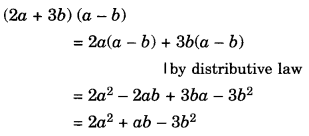
![]()
Question 14.
\left( a+4 \right) \left( a+2 \right) = { a}^{ 2 } + 8
Solution.
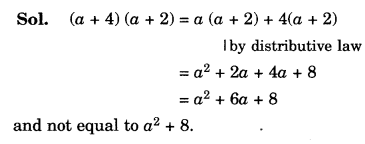
Question 15.
\left( a-4 \right) \left( a-2 \right) = { a}^{ 2 }-8
Solution.
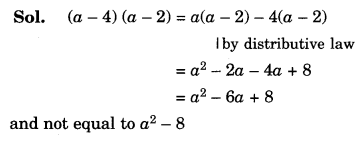
Question 16.
\frac { { 3x }^{ 2 } }{ { 3x }^{ 2 } } =0
Solution.
\frac { { 3x }^{ 2 } }{ { 3x }^{ 2 } } =1 and not equal to 0
Question 17.
\frac { { 3x }^{ 2 }+1 }{ { 3x }^{ 2 } } =1+1=2
Solution.
\frac { { 3x }^{ 2 }+1 }{ { 3x }^{ 2 } } =\frac { { 3x }^{ 2 } }{ { 3x }^{ 2 } } +\frac { 1 }{ { 3x }^{ 2 } }
=1+\frac { 1 }{ { 3x }^{ 2 } } and not equal to 1 + 1 = 2
Question 18.
\frac { 3x }{ 3x+2 } =\frac { 1 }{ 2 }
Solution.
\frac { 3x }{ 3x+2 } =\frac { 3x }{ 3x+2 } and not equal to \frac { 1 }{ 2 }
Question 19.
\frac { 3 }{ 4x+3 } =\frac { 1 }{ 4x }
Solution.
\frac { 3 }{ 4x+3 } =\frac { 3 }{ 4x+3 } and not equal to \frac { 1 }{ 4x }
Question 20.
\frac { 4x+5 }{ 4x } =5
Solution.
\frac { 4x+5 }{ 4x } =\frac { 4x }{ 4x } +\frac { 5 }{ 4x } =1+\frac { 5 }{ 4x } and not equal to 5
Question 21.
\frac { 7x+5 }{ 5 } =7x
Solution.
\frac { 7x+5 }{ 5 } =\frac { 7x }{ 5 } +\frac { 5 }{ 5 } =\frac { 7x }{ 5 } +1 and not equal to 7x