Class 8 Maths NCERT Solutions Chapter 1 – Rational Numbers

Class 8 Maths NCERT Solutions Chapter 1: Rational Numbers

Ex – 1.1

Question 1.
Using appropriate properties find:
(i) −25×35+52−35×16
(ii) 25×(−37)−16×32+114×25
Solution.

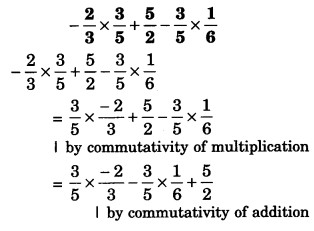
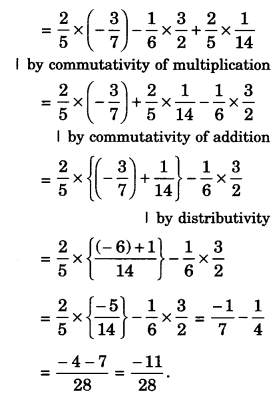
Question 2.
Write the additive inverse of each of the following:

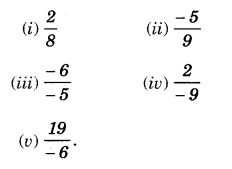
Solution.
(i) 28
Additive inverse of 28 is 28

(ii) −59
−6−5=65
Additive inverse of −6−5 is −65

(iii) −6−5
−6−5=65
Additive inverse of −6−5 is −65

(iv) 2−9
Additive inverse of 2−9 is 29

(v) 19−6
Additive inverse of  19−6 is 196

Question 3.
Verify that – (-x) = x for :
(i) x=1115
(ii) x=−1317
Solution.

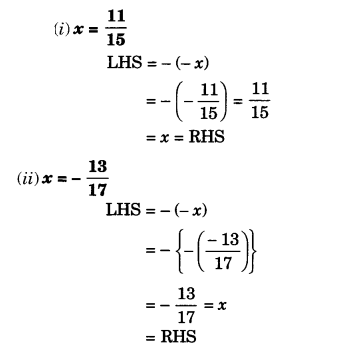
Question 4.
Find the multiplicative inverse of the following:

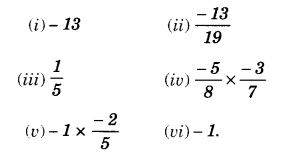
Solution.

Question 5.
Name the property under multiplication used in each of the following:
(i) −45×(1)=1×−45=−45
(ii) −1317×−27=−27×−1317
(iii) −1929×29−19=1
Solution.
(i) 1 is the multiplicative identity
(ii) Commutativity of multiplication
(iii) Multiplicative inverse.

Question 6.
Multiply 613 by the reciprocal of −716
Solution.
Reciprocal of −716 is −167
Now,
613×−167=6×(−16)13×7=−9691

Question 7.
Tell what property allows you to compute : 13×(6×43) as (13×6)×43
Solution.
Associativity.

Question 8.
Is the 89 multiplicative inverse of −118 ? Why or why not?
Solution.
−118=−98
Now, 89×−98=−1≠1
So, No ; 89 is not the multiplicative inverse of −118(=−98) because the product of 89 and -13(-) and −118(=−98) is not 1.

Question 9.
Is 0.3 the multiplicative inverse of 313 ? Why or why not?
Solution.
Yes ; 0.3 is the multiplicative inverse of 103 because
310×103=3×1010×3=3030=1

Question 10.
Write :
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
Solution.
(i) The rational number ‘0′ does not have a reciprocal.

(ii) The rational numbers 1 and (-1) are equal to their own reciprocals.

(iii) The rational number 0 is equal to its negative.

Question 11.
Fill in the blanks :
(i) Zero has……….reciprocal.
(ii) The numbers……….and………are their own reciprocals.
(iii) The reciprocal of – 5 is.………….
(iv) Reciprocal of 1x, where x≠0
(v) The product of two rational numbers is always a.………
(vi) The reciprocal of a positive rational number is……….
Solution.
(i) Zero has no reciprocal.
(ii) The numbers 1 and -1 are their own reciprocals.
(iii) The reciprocal of – 5 is −15
(iv) Reciprocal of 1x, where x≠0 is x.
(v) The product of two rational numbers is always a rational number.
(vi) The reciprocal of a positive rational number is positive.

Ex – 1.2

Question 1.
Represent these numbers on the number line.
(i) 74
(ii) −56
Solution.
(i) 74
We make 7 markings of distance 14 each on the right of 0 and starting from 0. The seventh marking represents 74

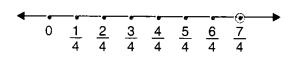
(ii) −56
We make 5 markings of distance 16 each on the right of 0 and starting from 0. The seventh marking represents −56

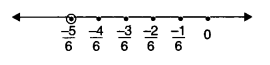
Question 2.
Represent −211,−511,−911 on the number line.
Solution.
We make 9 markings of distance 111 each on the left of 0 and starting from 0.
The second marking represents −211 the fifth marking represents −511 and the ninth marking represents −911

Question 3.
Write five rational numbers which are smaller than 2.
Solution.
Five rational numbers which are smaller than 2 are 1, 12,0, -1, −12

Question 4.
Find ten rational numbers between −25 and 12
Solution.

Question 5.
Find five rational numbers between:

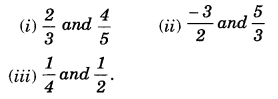
Solution.

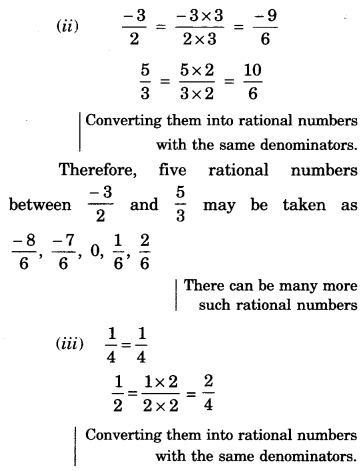
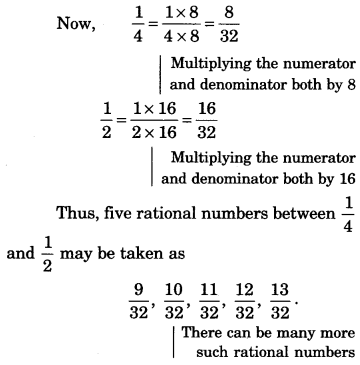
Question 6.
Write five rational numbers greater than -2.
Solution.
Five rational numbers greater than -2 are:
−32, -1, −12, 0, 12
There can be many more such rational numbers

Question 7.
Find ten rational numbers between 35 and 34
Solution.