Class 11 Maths NCERT Solutions Chapter 4: Principle of Mathematical Induction
Ex – 4.1
Question 1:
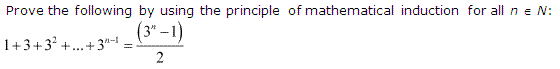
Ans :
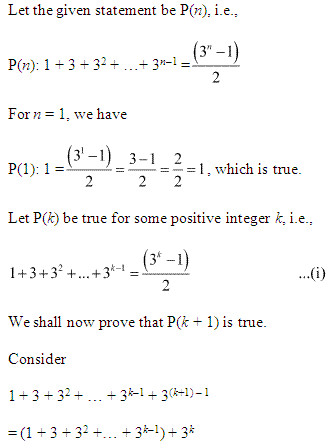

Question 2:
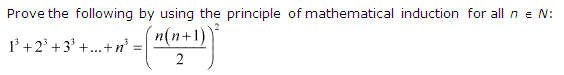
Ans :
Let the given statement be P(n), i.e.,
P(n) = 13 + 23 + 33 + …………. + n3 = (n(n+1)2)2.
For n = 1, we have
P(1) : 13 = 1
= (1(1+1)2)2=(122)2
= 12 = 1 which is true.
Let P(k) be true for some positive integer k, i.e.,
13 + 23 + 33 + …………. + k3 = (k(k+1)2)2
We shall now prove that P(k+1) is true.
Consider 13 + 23 + 33 + …………. + k3 = (k(k+1)2)2

Question 3:
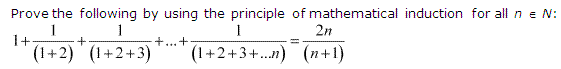
Ans :
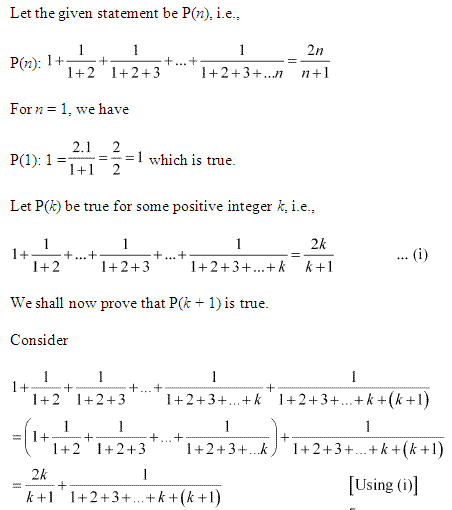

Question 4:
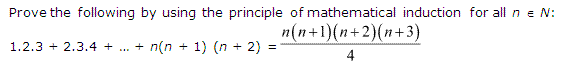
Ans :
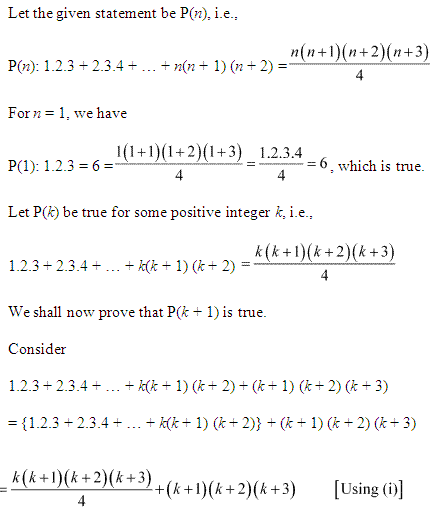

Question 5:
Ans :

Question 6:
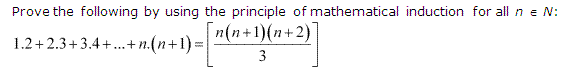
Ans :
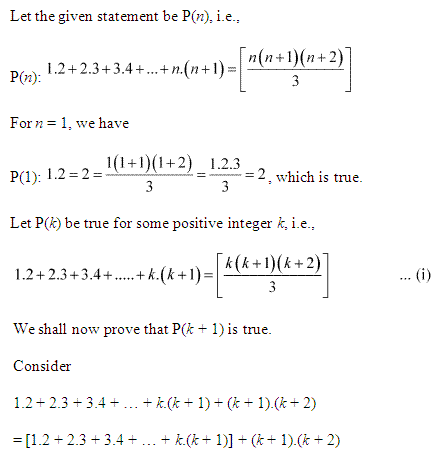
= k(k+1)(k+2)3 + (k + 1) (k + 2)
= (k + 1) (k + 2) + (k3 + 1)
= (k+1)(k+2)(k+3)3
= (k+1)(k+1+1)(k+1+2)3
Thus, P(k+1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 7:
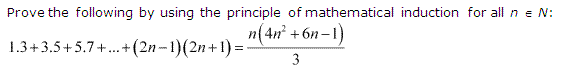
Ans :
Let the given statement be P(n), i.e.,
P(n) : 1 . 3 + 3 . 5 + 5 . 7 + … + (2n – 1) (2n + 1) = n(4n2+6n−1)3
For n = 1, we have
P(1) : 1 . 3 = 3
= 1(4.12+6.1−1)3=4+6−13=93 = 3, which is true.
Let P(k) be true for some positive integer k, Le.,
1 . 3 + 3 . 5 + 5 . 7 + ………………. + (2k – 1) (2k + 1) = k(4k2+6k−1)3 ……………(i)
We shall now prove that P(k + 1) is true.
Consider (1 . 3 + 3 . 5 + 5 . 7 + … + (2k – 1) (2k + 1) +{2 (k + 1) – 1} {2(k + 1) + 1}

Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, .statement P(n) is true for all natural numbers i.e., n.
Question 8:
![]()
Ans :
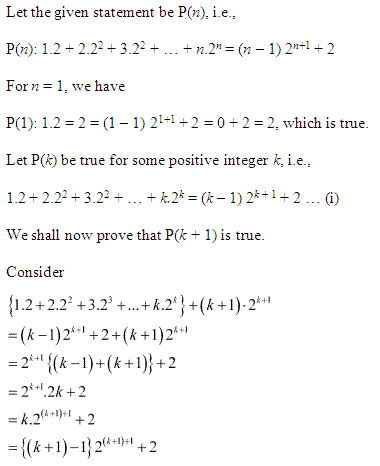

Question 9:
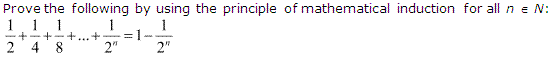
Ans :
Let the given statement be P(n), i.e.,
P(n) : 12+14+18+…+12n=1−12n
For n = 1, we have
P(1) : 12
= 1 – 121
= 12, which is true.
Let P(k) be true for some positive integer k, i.e.,
12+14+18+…+12k=1−12k
We shall now prove that P(k + 1) is true.
Consider (12+14+18+…+12k)+12k+1
= (1−12k)+12k+1
= 1−12k+122k=1−12k(1−12)
= 1−12k(12)=1−12k+1
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 10:
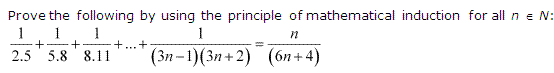
Ans :
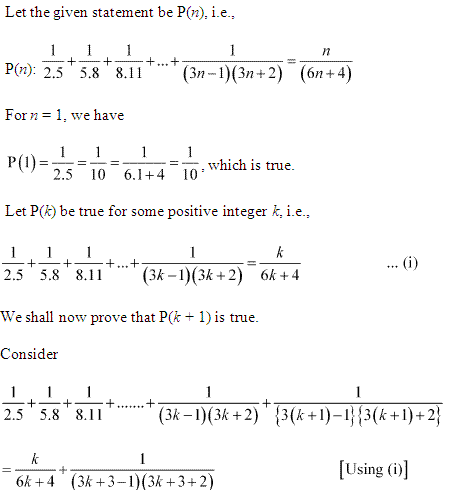

Question 11:
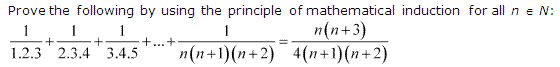
Ans :
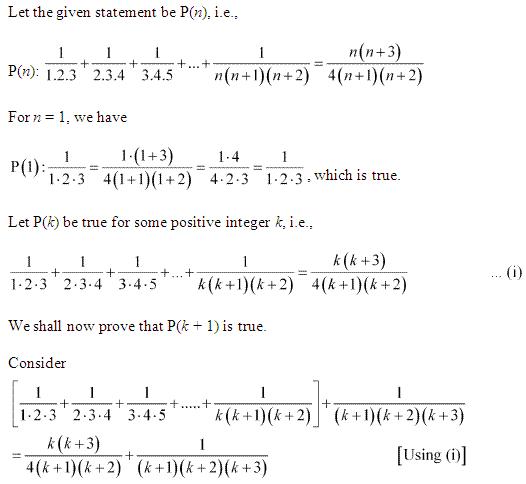
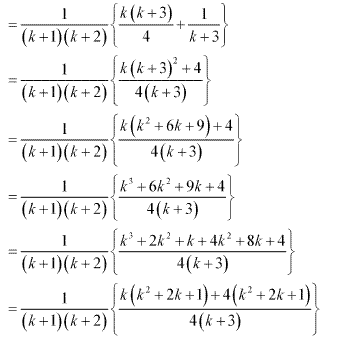

Question 12:

Ans :
Let the given statement be P(n), i.e.,
P(n) : a + ar + ar2 + …………… + arn – 1 = a(rn−1)r−1
For n = 1, we have
P(1) : a = a(r1−1)(r−1) = a, which is true.
Let P(k) be true for some positive integer k, i.e.,
a + ar + ar2 + …………… + ark – 1 = a(rk−1)r−1 …………..(i)
We shall now prove that P(k + 1) is true.
Consider
a + ar + ar2 + …………… + ark – 1} + ar(k + 1) – 1 = a(rk−1)r−1 + ark [Using eQuestion (i)]
= a(rk−1)+ark(k−1)r−1
= a(rk−1)+ark+1−arkr−1
= ark−a+ark+1−arkr−1=ark+1−ar−1
= a(rk+1−1)r−1
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 13:
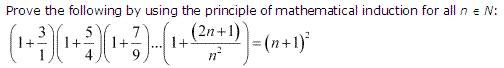
Ans :
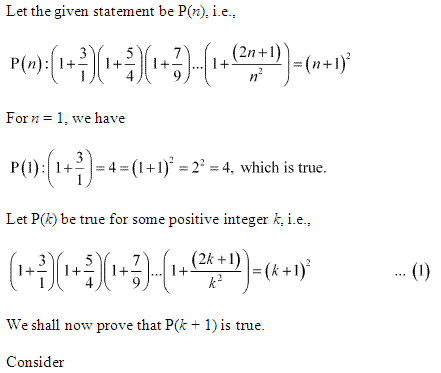

Question 14:
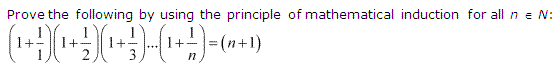
Ans :

Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 15:
Prove the following by using the principle of mathematical indcution for all n ∈ N:
12 + 32 + 52 + … + (2n – 1)2 = n(2n−1)(2n+1)3
Ans :
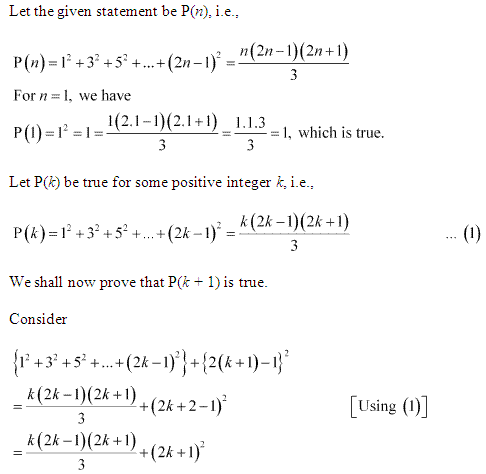

Question 16:
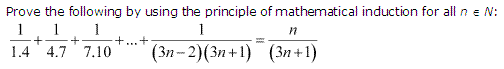
Ans :


Question 17:
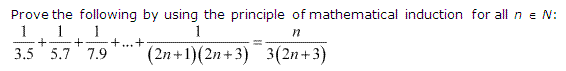
Ans :
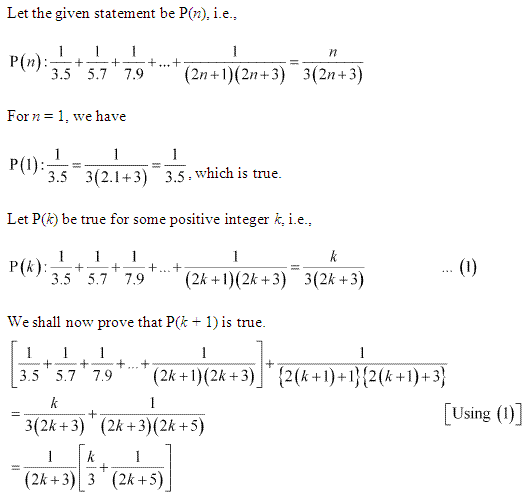

Question 18:

Ans :

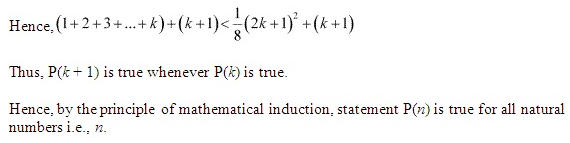
Question 19:
![]()
Ans :
Let the given statement be P(n), i.e.,
P(n) : n (n + 1) (n + 5) which is a multiple of 3.
It can be noted that P(n) is true for n=l since 1 (1 + 1) (1 + 5) = 12, which is a multiple of 3.
Let P(k) be true for some positive integer k, i.e., k (k + 1) (k + 5) is a multiple of 3.
∴ k (k + 1) (k + 5) = 3m, where m ∈ N ……………….(i)
We shall now prove that P(k + 1) is true whenever P(k) is true.
Consider (k + 1) {(k +1 ) + 1} {(k + 1) + 5}
= (k + 1) (k + 2) {(k + 5) + 1}
= (k + 1) (k + 2) (k + 5) + (k + 1) (k + 2)
= {k (k + 1) (k + 5) + 2 (k + 1) (k + 5)} + (k +1) (k + 2)
= 3m + (k + 1) {2 (k + 5) + (k + 2)}
= 3m + (k + 1) {2k +10 + k + 2}
= 3m + (k + 1) (3k + 12)
= 3m + 3 (k + 1) (k + 4)
= 3 {m + (k + 1) (k + 4)}
= 3 × q, where, q = {m + (k +1) (k + 4)} is some natural number.
Therefore, (k +1) {(k +1) +1} {(k +1) + 5} is a multiple of 3.
Thus, P(k + 1) is trtie whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Question 20:
![]()
Ans :


Question 21:
![]()
Ans :


Question 22:
![]()
Ans :


Question 23:
![]()
Ans :
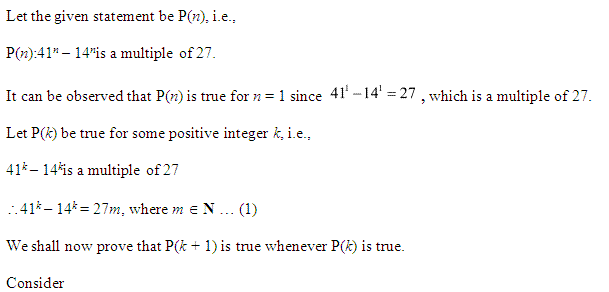

Question 24:
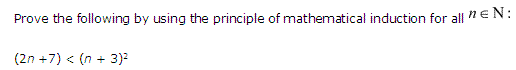
Ans :


Prove the following through the principle of mathematical induction for all values of n, where n is a natural number.
1) 1+3+3²+….+3n-1=\(\frac { { (3 }^{ n }-1) }{ 2 } \)
2: 1³+2³+3³+……+n³ = (n(n+1)2)2
3: 1+11+2+11+2+3+……+11+2+3+…+n=2nn+1
4: 1.2.3+2.3.4+…+n(n+1)(n+2)= \(\frac { n(n+1)(n+2)(n+3) }{ 4 } \)
5: 1.3+2.32+3.33+…+n.3n
