Class 11 Maths NCERT Solutions Chapter 3: Trigonometric Functions

---

Ex 3.1 

Q.1:Find the radian measures corresponding to the following degree measures:
(i) 25°
(ii) – 47° 30′
(iii) 240°
(iv) 520°
Solution:

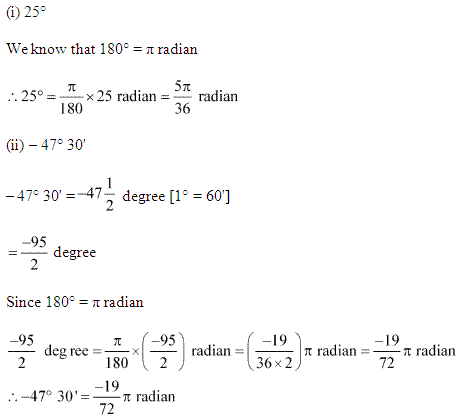
Q.2:

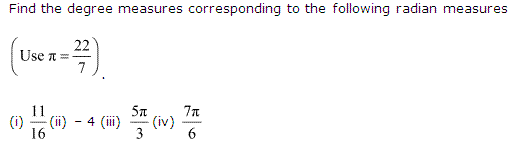
Solution:(i) 1116
We know that: π radian = 180°
∴ 1116 radain = 180π×1116 × degree

= 45×11π×4 degree

= 45×11×722×4 degree

= 3158 degree

= 39 38 degree

= 39° + 3×608 minutes [1° = 60′]

= 39° + 22′ + 12 minutes

= 39°22’30” [1′ = 60°].

Q.3:
A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Solution:
Number of revolutions made by the wheel in 1 minute = 360
∴ Number of revolutions made by the wheel in 1 second = 3606 = 6
In one complete revolution, the wheel turns an angle of 2π radian.
Hence, in 6 complete revolutions, it will turn an angle of 6 × 2π radian, i.e., 12π radian
Thus, in one second, the wheel turns an angle of 12π radian.
Q.4:
Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm y an arc of length 22 cm (Use π = 227).
Solution:

We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then θ = lr
Therefore, for r = 100 cm, l = 22 cm,
we have

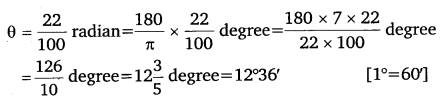
Thus, the required angle is 12°36′.

Q.5:
In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
Solution:

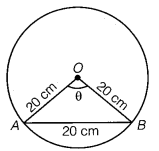
Given, diameter = 40 cm
∴ radius (r) = 402 = 20 cm
and length of chord, AB = 20 cm
Thus, ∆OAB is an equilateral triangle.
We know that,
θ =  Arc AB radius 
⇒ Arc AB = θ × r
= π3 × 20 .
= 203 π cm.

Q.6:
If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.
Solution:

Let the radii of the two circles be r₁ and r₂.
Let an arc of length l subtend an angle of 60° at the centre of the circle of radius r₁, while let an arc of length l subtend an angle of 75° at the centre of the circle of radius r₂.
Now, 6o° = π3 radian and
75° = 5π12 radian
We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then θ = lr or l = rθ
∴ l = r1π3 and

l = r25π12

⇒ r1π3=r25π12

⇒ r = r254

r1r2=54
Thus, the ratio of the radii is 5 : 4.

Q.7:
Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm
(ii) 15 cm
(iii) 21 cm.
Solution:

We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then
θ = lr.
It is given that r = 75 cm

(i) Here, l = 10 cm
θ = 1075 radian
= 215 radian

(ii) Here, l = 15 cm
θ = 1575 radian
θ = 15 radian

(iii) Here, l = 21 cm
θ = 2175 radian
= 775 radian.

NCERT Solutions for Class 11 Maths Chapter 3 Exercise 3.2

Q.1:
Find the values of other five trigonometric functions if cos x = – 12 x lies in third quadrant.
Solution:

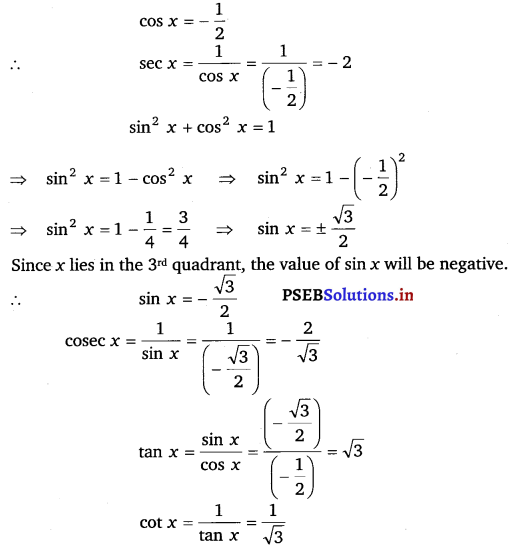
Q.2:
Find the values of other five trigonometric functions if sin x = 35, x lies in second quadrant.
Solution:

sin x = 35

cosec x = 1sinx=1(35)=53
sin² x + cos² x = 1
⇒ cos² x = 1 – sin² x
⇒ cos² x = 1 – (35)²

⇒ cos² x = 1 – 925

⇒ cos² x = 1625

⇒ cos x = ± 45
Since x lies in the 2nd quadrant, the value of cos x will be negative

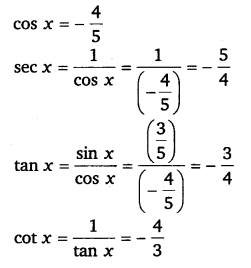
Q.3:
Find the values of other five trigonometric functions if cot x = 34, x lies in third quadrant.
Solution:

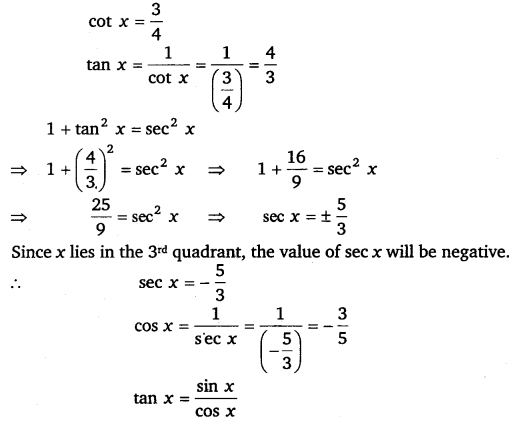
⇒ 43=sinx−35
⇒ sin x = (43)×(−35)=−45
⇒ cosec x = 1sinx=−54.

Q.4:
Find the values of other five trigonometric functions if sec x = 135, x lies in fourth quadrant.
Solution:

Q.5:
Find the values of other five trigonometric functions if tan x = 512, x lies in second quadrant.
Solution:

tan x = – 512

cot x = 1tanx=1(−512)=−125

1 + tan² x = sec² x

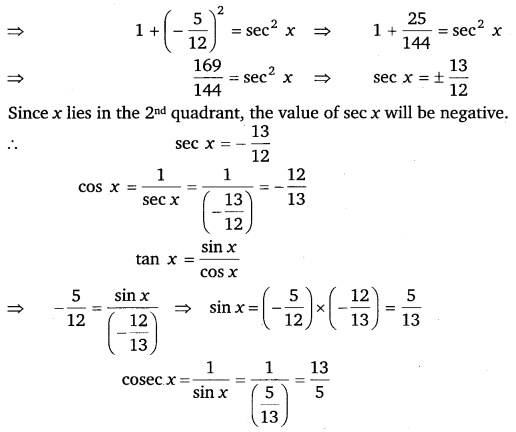
Q.6:
Find the value of the trigonometric function sin 765°.
Solution:
It is known that the values of sin x repeat after an interval of 2π or 360°.
∴ sin 765° = sin (2 × 360° + 45°)
= sin 45° = 1
Q.7:
Find the value of the trigonometric function cosec (- 1410°)
Solution:
It is known that the values of cosec x repeat after an interval of 2π or 360°.
∴ cosec (- 1410°) = cosec (- 1410° + 4 x 360°)
= cosec (- 1410° + 1440°)
= cosec 30° = 2.
Q.8:
Find the value of the trigonometric function tan 19π3.
Solution:

It is known that the values of tan x repeat after an interval of π or 180°.
∴ tan19π3=tan613π

= tan(6π+π3)=tanπ3

= tan 60° = √3.

Q.9:
Find the value of the trigonometric function sin (−11π3).
Solution:

It is known that the values of cot x repeat after an interval of π or 180°.

∴ sin(11π3)=sin(−11π3+2×2π)

= sin(π3)=sin60∘=3√2

Q.10:
Find the value of the trigonometric function cot (−15π4).
Solution:

It is known that the values of cot x repeat after an interval of ir or 1800.
∴ cot(−15π4)=cot(−15π4+4π)=cotπ4 = 1.

NCERT Solutions for Class 11 Maths Chapter 3 Exercise 3.3

Q.1:

Prove that: sin² π6 + cos² π3 – tan² π4 = – 12
Solution:

L.H.S.= sin² π6 + cos² π3 – tan² π4

= (12)2+(12)2 – (1)²

= 14+14−1=−12

= R.H.S.
Hence proved.

Q.2:
Prove that: 2 sin² π6 + cosec² 7π6 cos² π3 = 32
Solution:

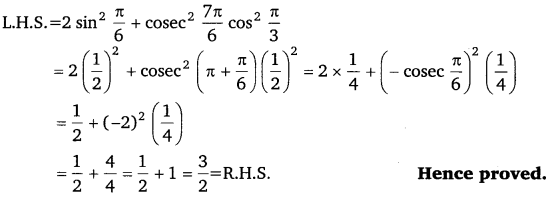
Q.3:
Prove that :cot² π6 + cosec 5π6 + 3 tan² π6 = 6
Solution:

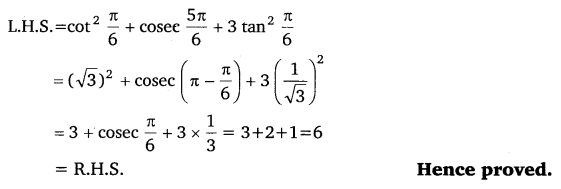
Q.4:
Prove that: 2 sin² 3π4 + 2 cos² π4 + 2 sec² π3 = 10
Solution:

L.H.S = 2sin23π4+2cos2π4+2sec2π3

= 2{sin(π−π4)}2+2(12√)2+2(2)2

= 2{sinπ4}2+2×12+8

= 2 (12√)2 + 1 + 8

= 1 + 1 + 8
= 10 = R.H.S.
Hence proved.

Q.5:
Find the value of: (i) sin 75°,
(ii) tan 15°
Solution:

(i) sin 75° sin (45° + 30°)
= sin 45° cos 30° + cos 45° sin 30°
[∵ sin (x + y) = sin x cos y + cos x sin y]
= (12√)(3√2)+(12√)(12)

= 3√22√+122√=3√+122√

(ii) tan 15° = tan (45° – 30°)

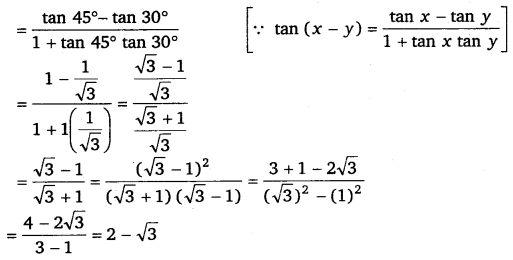
Q.6:
cos(π4−x)cos(π4−y)−sin(π4−x)sin(π4−y) = sin (x + y)
Solution:

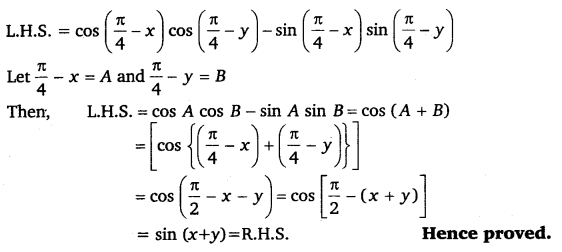
Q.7:
Prove that: tan(π4+x)tan(π4−x)=(1+tanx1−tanx)2
Solution:

= (1+tanx1−tanx)2
= R.H.S
Hence proved.
Q.8:
Prove that: cos(π+x)cos(−x)sin(π−x)cos(π2+x) = cot² x
Solution:

L.H.S = cos(π+x)cos(−x)sin(π−x)cos(π2+x)

= [−cosx][cosx](sinx)(−sinx)=−cos2x−sin2x

= cot² x

= R.H.S
Hence proved.

Q.9:
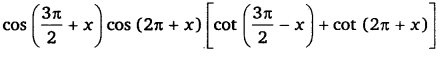 = 1
Solution:

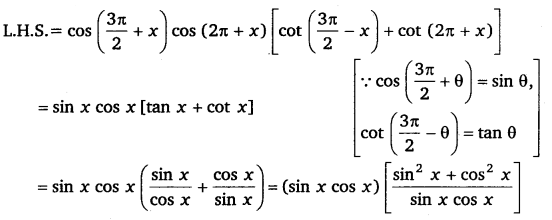
= 1 = R.H.S
Hence proved.
Q.10:
Prove that: sin (n + 1) x sin (n + 2) x + cos (n + 1) x cos (n + 2) x = cos x
Solution:
L.H. S. = sin (n + 1 )x sin (n + 2) x + cos (n +1) x cos (n + 2) x
[By the formula, cos (A – B) = cos A cos B + sin A sin B]
= cos [(n + 2) x + (n + 1) x]
= cos (4x + 2x – 4x – x)
= cos x = R.H.S.
Hence proved.
EQ.11:
Prove that: cos(3π4+x)−cos(3π4−x)=−2–√sinx
Solution:

It is known that
cos A – cos B = −2sin(A+B2)⋅sin(A−B2)

∴ L.H.S.= =cos(3π4+x)−cos(3π4−x)

= –2sin{(3π4+x)+(3π4−x)2}⋅sin{(3π4+x)−(3π4−x)2}

= – 2 sin (3π4) sin x

= – 2 sin (- π4) sin x

= – √2 sin x = R.H.S.
Hence proved.

Q.12:
Prove that: sin² 6x – sin² 4x = sin 2x sin 10 x
Solution:

It is known that
sin A + sin B = 2 sin(A−B2)cos(A−B2)

sin A – sin B = 2 cos(A+B2)sin(A−B2)
L.H.S.= sin² 6x – sin² 4x
= (sin 6x + sin 4x) (sin 6x – sin 4x)
= (2 sin 5x cos x) (2 cos 5x sin x)
= (2 sin 5x cos 5x) (2 sin x cos x)
= sin 10x sin 2x = R.H.S.
Hence proved.

Q.13:
Prove that: cos² 2x cos² 6x = sin 4x sin 8x
Solution:

It is known that
cos A + cos B = 2 cos(A+B2)cos(A−B2)

cos A – cos = 2 sin(A+B2)sin(A−B2)

∴ L.H.S = cos² 2x – cos² 6x
= (cos 2x + cos 6x) (cos 2x – 6x)
= [2cos(2x+6x2)cos(2x−6x2)][−2sin(2x+6x2)sin(2x−6x)2]
∴ L.H.S.= cos² 2x – cos² 6x
= (cos 2x + cos 6x) (cos 2x – 6x)
= [2 cos 4x cos (-2x)] [- 2 sin 4x sin (- 2x)]
= [2 cos 4x cos 2x] [- 2 sin 4x (- sin 2x)]
= (2 sin 4x cos 4x) (2 sin 2x cos 2x)
= sin 8x sin 4x
= R.H.S.
Hence proved.

Q.14:
Prove that: sin 2x + 2 sin 4x + sin 6x = 4 cos² x sin 4x
Solution:
L.H.S.= sin 2x + 2 sin 4x + sin 6x
= [sin 2x + sin 6x] + 2 sin 4x
= [2sin(2x+6x2)cos(2x−6x2)] + 2 sin 4x
[∵ sin A + sin B = 2 sin(A+B2)cos(A−B2)]
= 2 sin 4x cos (- 2x) + 2 sin 4x
= 2 sin 4x cos 2x + 2 sin 4x
= 2 sin 4x (cos 2x + 1)
= 2 sin 4x (2 cos² x – 1 + 1)
= 2 sin 4x (2 cos² x)
= 4 cos² x sin 4x
= R.H.S.
Hence proved.
Q.15:
cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)
Solution:

Q.16:
Prove that: cos9x−cos5xsin17x−sin3x=−sin2xcos10x
Solution:

Q.17:
Prove that: sin5x+sin3xcos5x+cos3x = tan 4x
Solution:

It is known that
sin A + sin = 2 sin(A+B2)cos(A−B2)

cos A + cos = 2 cos(A+B2)cos(A−B2)

∴ L.H.S = sin5x+sin3xcos5x+cos3x

= 2sin(5x+3x2)cos(5x−3x2)2cos(5x+3x2)cos(5x−3x2)

= 2sin4xcosx2cos4xcosx=sin4xcos4x

= tan 4x = R.H.S.
Hence proved.

Q.18:
Prove that: sinx−sinycosx+cosy=tanx−y2.
Solution:

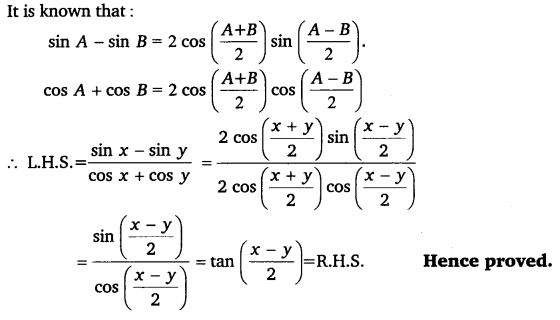
Q.19:
Prove that: sinx+sin3xcosx+cos3x = tan 2x
Solution:

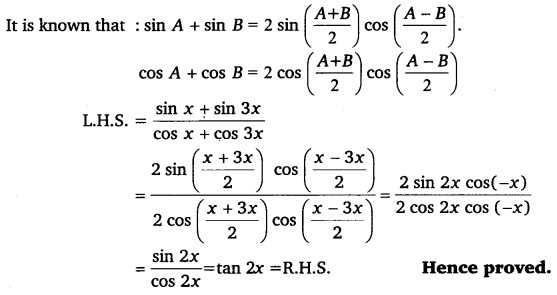
Q.20:
Prove that: sinx−sin3xsin2x−cos2x = 2 sin x
Solution:

It is known that
sin A – sin B = 2 cos(A+B2)sin(A−B2)

cos² A – sin² A = cos 2A

∴ L.H.S. = =sinx−sin3xsin2x−cos2x

= 2cos(x+3x2)sin(x−3x2)−cos2x

= 2cos2xsin(−x)−cos2x

= – 2 × (- sin x) = 2 sin x

= R.H.S

Hence proved.

Q.21:
Prove that: cos4x+cos3x+cos2xsin4x+sin3x+sin2x = cot 3x
Solution:

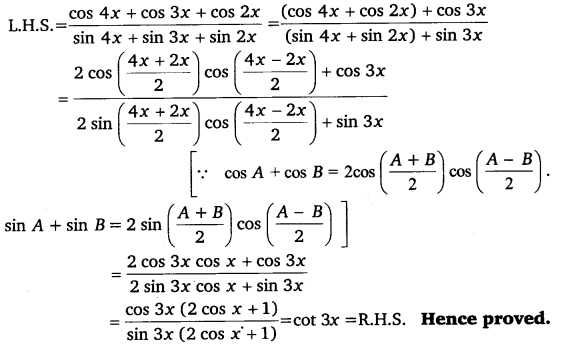
Q.22:
Prove that : cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1
Solution:
L.H.S.= cot x cot 2x – cot 2x cot 3x – cot 3x cot x
= cot x cot 2x – cot 3x (cot 2x + cot x)
= cot x cot 2x – cot (2x + x) (cot 2x + cot x)
= cot x cot 2x – [cot2xcotx−1cotx+cot2x] (cot 2x + cot x)
[∵ cot (A + B) = cotAcotB−1cotA+cotB]
= cot x cot 2x – (cot 2x cot x – 1)
= 1 = R.H.S.
Hence proved.
Q.23:
Prove that: tan 4x = 4tanx(1−tan2x)1−6tan2x+tan4x.
Solution:
It is known that:
tan 2A = 2tanA1−tan2A

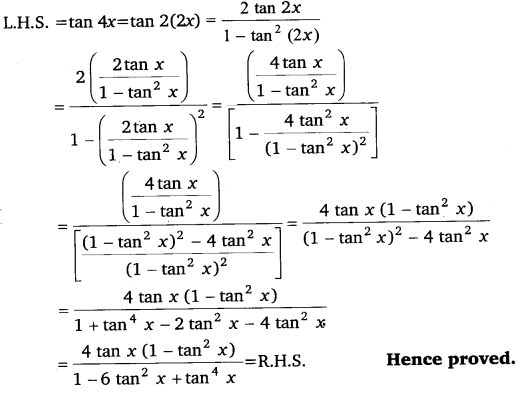
Q.24:
Prove that: cos 4x = 18 sin² x cos² x
Solution:
L.H.S. = cos 4x = cos 2(2x)
= 1 – 2 sin² 2x [∵ cos 2A = 1 – 2 sin² A]
= 1 – 2(2 sin x cos x)² [∵ sin 2A = 2 sin A cos A]
= 1 – 8 sin² x cos² x
= R.H.S.
Hence proved.
Q.25:
Prove that: cos 6x = 32 cos⁶ x – 48 cos⁴ x + 18 cos² x – 1
Solution:
We know that: cos 3x = 4 cos³ x – 3cos x
On replacing x by 2x, we get
cos 3(2x) = 4 cos³ (2x) – 3 cos 2x
⇒ cos 6x = 4 (2cos² x – 1)³ – 3 (2cos² x – 1)
[∵ cos 2x = 2cos² x – 1]
= 4 [8 cos⁶ x – 12 cos⁴ x + 6 cos² x – 1] – 6 cos² x + 3
[∵ (a – b)³ = a³ – 3a²b + 3ab² – b³]
= 32 cos⁶ x – 48 cos⁴ x + 24 cos² x – 4 – 6 cos² x + 3
⇒ cos 6x = 32 cos⁶ x – 48 cos⁴ x + 18 cos² x – 1
Hence proved.

Class 11 Maths NCERT Solutions Chapter 3 Exercise 3.4

Q.1:
Find the principal and general solutions of the equation, tan x = √3
Solution:
tan x = √3
It is known that:
tan π3 = √3 and
tan (4π3) = tan ( π + π3)
= tan π3 = √3
Therefore, the principal solutions are x = π3 and 4π3.
Now, tan x = tan π3
⇒ x = nπ + π3, where n ∈ Z
Therefore, the general solution is x = nπ + π3, where n ∈ Z.
Q.2:
Find the principal and general solutions of the equation: sec x = 2
Solution:
sec x = 2
It is known that:
sec π3 = 2 and
sec 5π3 = sec (2π – π3)
= sec π3 = 2
Therefore, the principal solutions are x = π3 and 5π3.
Now, sec x = sec π3
cos x = cos π3 [∵ sec x = 1cosx]
⇒ x = 2nπ ± π3, where n e Z
Therefore, the general solution is x = 2nπ ± π3, where n ∈ Z.
Q.3:
Find the principal and general solutions of the equation cot cot x = – √3.
Solution: cot x = – √3

Q.4:
Find the principal and general solutions of cosec x = – 2
Solution: cosec x = – 2
It is known that:
cosec π6 = 2

Q.5:
Find the general solution of the equation: cos 4x = cos 2x
Solution:

cos 4x = cos 2x
cos 4x – cos 2x = 0
– 2 sin (4x+2x2) sin (4x−2x2) = 0

[∵ cos A – cos B = 2 \sin \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)]

sin 3x sin x = 0
sin 3x = 0or sin x = 0
3x = nπ or x = nπ, where n ∈ Z
x = nπ3 or x = nπ, where n ∈ Z.

Q.6:
Find the general solution of the equation cos 3x + cosx – cos 2x = 0
Solution:

cos 3x + cos x – cos 2x = 0
2 cos (3x+x2) cos (3x−x2) – cos 2x = 0

[∵ cos A + cos B = 2 cos(A+B2)cos(A−B2)]

2 cos 2x cos x – cos 2x = 0
cos 2x (2 cos x – 1) = 0
cos 2x = 0 or 2 cos x – 1 = 0
cos 2x = 0 or cos x = \(\frac{1{2}\)
∴ 2x = (2n + 1) π2 or cos x = cos π3, where n ∈ Z
x = (2n + 1) π4 or x = 2nπ ± π3 where n ∈ Z.

Q.7:
Find the general solution of the equation sin 2x + cos x = 0
Solution:

sin 2x + cos x = 0
⇒ 2sin x cos x + cos x = 0
⇒ cos x (2 sin x + 1) = 0
⇒ cos x = 0 or 2 sin x + 1 = 0
Now, cos x = 0
⇒ x = (2n + 1) π2 , where n ∈ Z.
or 2 sin x + 1 = 0
⇒ sin x = – 12

= – sin π6

= sin (π + π6)

= sin 7π6

x = nπ + (- 1)ⁿ 7π6 where n ∈ Z
Therefore, the general solution is (2n + 1) π2 or nπ + (- 1)ⁿ 7π6 where n ∈ Z.

Q.8:
Find the general solution of the equation sec² 2x = 1 – tan 2x.
Solution:

sec² 2x = 1 – tan 2x
1 + tan² 2x = 1 – tan 2x
tan² x + tan 2x = 0
=> tan 2x (tan 2x + 1) = 0
=> tan 2x = 0 or tan 2x + 1 = 0
Now, tan 2x = 0
=> tan 2x = tan 0
2x = nπ + 0, where n ∈ Z
x = nπ2, where n ∈ Z
or tan 2x + 1 = 0
= tan 2x = – 1
= – tan π4

= tan (π – π4)

= tan 3π4

2x = nπ + 3π4 where n ∈ Z

x = nπ2+3π8, where n ∈ Z

Therefore, the general solution is nπ2 or nπ2+3π8 where n ∈ Z.

Q.9:
Find the general solution of the equation sin x + sin 3x + sin 5x = 0
Solution:

sin x + sin 3x + sin 5x = 0
⇒ (sin x + sin 5x) + sin 3x = 0

[2sin(x+5x2)cos(x−5x2)] + sin 3x = 0

[∵ sin A + sin B = 2 sin sin(A+B2)cos(A−B2)]

2 sin 3x cos (2x) + sin 3x = 0
2 sin 3x cos 2x + sin 3x = 0
sin 3x (2 cos 2x +1) = 0
sin 3x = 0 or 2 cos 2x + 1 = 0
Now sin 3x = 0
⇒ 3x = nπ, where n ∈ Z
i.e., x = nπ3 where n ∈ Z
or 2 cos 2x + 1 = 0
cos 2x = −12

= – cos π3

= cos (π – π3)

cos 2x = cos 2π3

⇒ 2x = 2nπ ± 2π3, where n ∈ Z

⇒ x = nπ ± π3, where n ∈ Z

Therefore, the general solution is nπ3 or nπ ± π3, where n ∈ Z.

NCERT Solutions for Class 11 Maths Chapter 3 Miscellaneous Exercise

Q.1:
Prove that:
2cosπ13cos9π13+cos3π13+cos5π13 = 0
Solution:

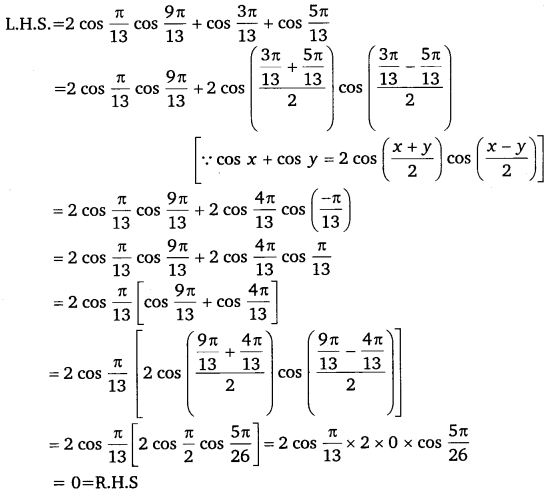
Hence proved.
Q.2:
Prove that: (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0.
Solution:

L.H.S. = (sin 3x + sin x) sin x + (cos 3x – cos x) cos x
= sin 3x sin x + sin² x + cos 3x cos x – cos² x
= cos 3x cos x + sin 3x sin x – (cos² x – sin² x)
= cos (3x – x) – cos 2x
[∵ cos(A – B) = cos A cos B + sin A sin B]
= cos 2x – cos 2x = 0
=R.H.S.
Hence proved.

Q.3:

Prove that:
(cos x + cos y)² + (sin x – sin y)² = 4 cos² (x+y2)

Solution:

L.H.S.= (cos x + cos y)² + (sin x – sin y)²
= cos² x + cos² y + 2 cos x cos y + sin² x + sin² y – 2 sin x sin y
= (cos² x + sin² x) + (cos² y + sin² y) + 2 (cos x cos y – sin x sin y)
= 1 + 1 + 2 cos (x + y)
[∵ cos (A + B) = (cos A cos B – sin A sin B)]
= 2 + 2 cos (x + y)
= 2 [1 + cos (x + y)]
= 2[1 + 2cos2(x+y2) – 1]
[∵ cos 2A = 2 cos² A – 1]
= 4 c0s² (x+y2)
= R.H.S.
Hence proved.

Q.4:
Prove that:
(cos x – cos y)² + (sin x – sin y)² = 4 sin² x−y2
Solution:

L.H.S.= (cos x – cos y)² + (sin x – sin y)²
= cos² x + cos² y – 2 cos x cos y + sin² x + sin² y – 2 sin x sin y
= (cos² x + sin² x) + (cos² y + sin² y) – 2 [cos x cos y + sin x sin y]
= 1 + 1 – 2 [cos (x – y)]
= 2 [1 – {1 – 2 sin² (x−y2)}]
[∵ cos 2A = 1 – 2 sin² A]
= 4 sin² (x−y2)
= R.H.S.
Hence proved.

Q.5:
Prove that: sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x sin 4x
Solution:

It is known that sin A + sin B = 2 sin(A+B2)⋅cos(A−B2)
∴ L.H.S. = (sin x + sin 3x) + (sin 5x + sin 7x)
= (sin x + sin 5x) + (sin 3x + sin 7x)
= 2sin(x+5x2) . cos(x−5x2)+2sin(3x+7x2)cos(3x−7x2)
= 2 sin 3x cos (- 2x) + 2 sin 5x cos (- 2x)
= 2 sin 3x cos 2x + 2 sin 5x cos 2x
= 2 cos 2x [sin 3x + sin 5x]
= 2 cos 2x [latex]2 \sin \left(\frac{3 x+5 x}{2}\right) \cdot \cos \left(\frac{3 x-5 x}{2}\right)[/latex]
= 2 cos 2x [2 sin 4x . cos (- x)]
= 4 cos 2x sin 4x cos x
= R.H.S.
Hence proved.

Q.6:
Prove that: (sin7x+sin5x)+(sin9x+sin3x)(cos7x+cos5x)+(cos9x+cos3x) = tan 6x
Solution: It is known that

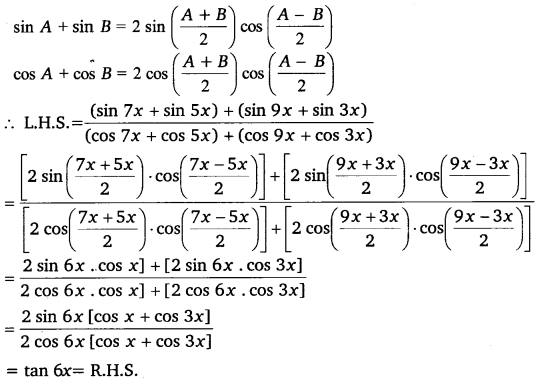
Hence proved.

Q.7:
Prove that: sin 3x + sin 2x – sin x = 4 sin x cos x2 cos 3x2.
Solution: L.H.S. = sin 3x + sin 2x – sin x
= sin 3x + (sin 2x – sin x)

Q.8:
Find sin x2, cos x2 and tan x2 for tan x = – 43, x in quadrant II.
Solution:

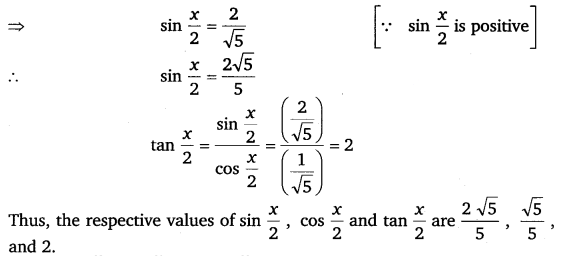
Q.9:
Find sin x2, cos x2 and tan x2 for cos x = – 13, x in quadrant III.
Solution:


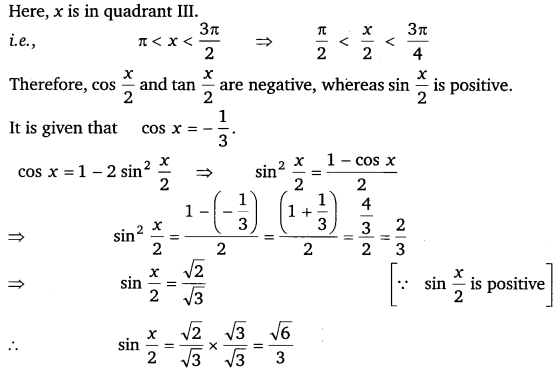
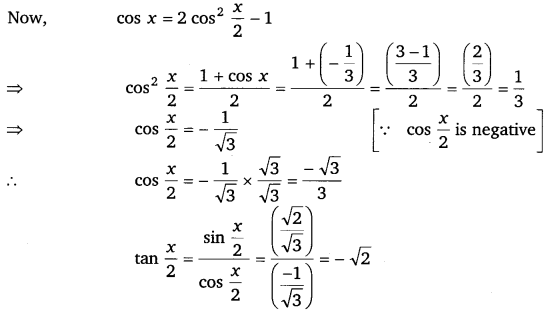
Thus, the respective values of sin x2, cos x2 and tan x2 are 6√5, 3√3 and – √2.

Q.10:
Find sin x2, cos x2 and tan x2 for sin x = 14, x in quadrant II.
Solution:

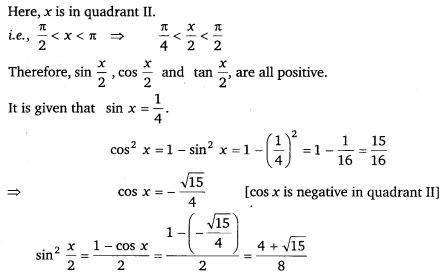
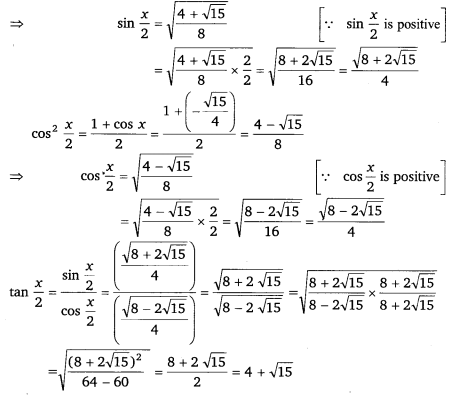
Thus, the respective values of sin x2, cos x2 and tan x2 are 8+215√4−−−−−−√, 8−215√4−−−−−−√ and 4 + √15.